模拟电路网络课件 第三十七节:基本运算电路

8.1  基本运算电路

一、反相比例运算放大电路

图 1  反相比例运算电路

反相输入放大电路如图1所示，信号电压通过电阻R1加至运放的反相输入端，输出电压vo通过反馈电阻Rf反馈到运放的反相输入端，构成电压并联负反馈放大电路。R ¢为平衡电阻应满足R ¢= R1//Rf。

利用虚短和虚断的概念进行分析，vI=0，vN=0，iI=0，则  

即      

∴

该电路实现反相比例运算。

反相放大电路有如下特点

1．运放两个输入端电压相等并等于0，故没有共模输入信号，这样对运放的共模抑制比没有特殊要求。

2．vN= vP，而vP=0，反相端N没有真正接地，故称虚地点。

3．电路在深度负反馈条件下，电路的输入电阻为R1，输出电阻近似为零。

二、同相比例运算电路

图 1  同相比例运算电路

同相输入放大电路如图1所示，信号电压通过电阻RS加到运放的同相输入端，输出电压vo通过电阻R1和Rf反馈到运放的反相输入端，构成电压串联负反馈放大电路。

根据虚短、虚断的概念有vN= vP= vS，i1= if

于是求得 

所以该电路实现同相比例运算。

同相比例运算电路的特点如下

1．输入电阻很高，输出电阻很低。

2．由于vN= vP= vS，电路不存在虚地，且运放存在共模输入信号，因此要求运放有较高的共模抑制比。

三、加法运算电路

图 1  加法运算电路

图1所示为实现两个输入电压vS1、vS2的反相加法电路，该电路属于多输入的电压并联负反馈电路。由于电路存在虚短，运放的净输入电压vI=0，反相端为虚地。利用vI=0，vN=0和反相端输入电流iI=0的概念，则有

 或   

由此得出

若R1= R2= Rf，则上式变为 –vO= vS1+ vS2

式中负号为反相输入所致，若再接一级反相电路，可消去负号，实现符 合 常规的算术加法。该加法电路可以推广到对多个信号求和。

从运放两端直流电阻平衡的要求出发，应取R´=R1//R2//Rf。

四、减法运算电路

1、反相求和式运算电路

图1所示是用加法电路构成的减法电路，第一级为反相比例放大电路，若Rf1=R1，则vO1= –vS1；第二级为反相加法电路，可以推导出 

若取R2= Rf2，则vO = vS1–vS2

由于两个运放构成的电路均存在虚地，电路没有共模输入信号，故允许vS1、vS2的共模电压范围较大。

2、差分式减法电路

差分式减法电路图1所示电路可以实现两个输入电压vS1、vS2相减,在理想情况下，电路存在虚短和虚断，所以有vI=0，iI=0，由此得下列方程式：

                                                                                                             图 1

及

由于vN=vP，可以求出

若取 ，则上式简化为

即输出电压vO与两输入电压之差（vS2–vS2）成比例，其实质是用差分式放大电路实现减法功能。

差分式放大电路的缺点是存在共模输入电压。因此为保证运算精度应当选择共模抑制比较高的集成运放。差分式放大电路也广泛应用于检测仪器中，可以用多个集成运放构成性能更好的差分式放大电路。

五、积分电路

图1a所示为基本积分电路。其输出电压与输入电压成积分运算关系。

利用虚地的概念：vI=0，iI=0，则有 即是电容C 的充电电流，

即  

则 

式中vo(t1)为t1时刻电容两端的电压值，即初始值。

积分运算电路的输出-输入关系也常用传递函数表示为

假设输入信号vs是阶跃信号，且电容C 初始电压为零，则当t≥0时

输出电压vO与时间t的关系如动画所示。

对于实际的积分电路，由于集成运放输入失调电压、输入偏置电流和失调电流的影响，常常会出现积分误差，可选用VIO、Im、IIO较小和低漂移的运放，或选用输入级为FET组砀BiFET运放。

积分电容器的漏电流也是产生积分误差的原因之一，因此，选用泄漏电阻大的电容器，如薄膜电容、聚苯乙烯电容器以减少积分误差。

图1所示的积分器可用作显示器的扫描电 路 或将方波转换为三角波等。

六、微分电路

1. 基本微分电路

微分是积分的逆运算，将基本积分电路中的电阻和电容元件位置互换，便得到图1所示的微分电路。

在这个电路中，同样存在虚地和虚断，因此可得

上式表明，输出电压vO与输入电压的微分 成正比。

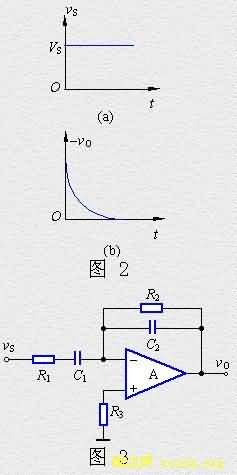
当输入电压vS为阶跃信号时，考虑到信号源总存在内阻，在t=0时，输出电压仍为一个有限值，随着电容器C的充电。输出电压vOo将逐渐地衰减，最后趋近于零，如图2所示。

2. 改进型微分电路

当输入电压为正弦信号vS=sinwt时，则输出电压vO=–RCwcoswt。此时vO的输出幅度将随频率的增加而线性地增加。说明微分电路对高频噪声特别敏感，故它的抗干扰能力差。另外，对反馈信号具有滞后作用的RC环节，与集成运放内部电路的滞后作用叠架在一起，可能引起自激振荡。再者vS突变时，输入电流会较大，输入电流与反馈电阻的乘积可能超过集成运主的最大输出电压，有可能使电路不能正常工作。一种改进型的微分电路如图3所示。其中R1起限流作用，R2和C2并联起相位补偿作用。该电路是近似的微分电路。

七、比例—积分—微分电路

对于基本积分电路，用Z1和Zf代替电阻和电容。在复频域中，应用拉氏变换，将Z1和Zf写成运算阻抗的形式Z1(s)、Zf(s)，其中s为复频率变量，输出电压的表达式可以写成

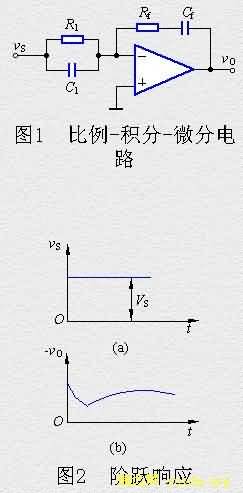
改变Z1(s)和Zf(s)的形式，可以实现各种不同的数学运算。对于图1a所示的电路，其传递函数为

上式括号内第一、二两项表示比例运算；第三项表示积分运算；因 表示积分；第四项表示微分运算，因 。图2b表示在输入阶跃信号情况下，输出电压的波形。

在自动控制系统中，比例-积分-微分运算经常用来组成 PID调节器。在常规调节中，比例运算、积分运算常用来提高调节精度，而微分运算则用来加速过渡过程。