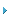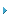带约束条件的函数化简
1、约束条件的定义
在一些逻辑电路中,经常遇到在真值表中对于变量的某些取值,函数值可以任意的,或者这些变量根本不会出现。
例如一个电路的输入为8421BCD码,则其输入变量中的16种组合中1010~1111始终不会出现。
由于这些输入组合不可能出现或输出在这些组合的情况下不管为0还是为1无所谓,则将这些输入组合称为约束条件、约束项或任意项。在存约束项的卡诺图或真值表中对应的输出用φ、×或d来表示。在函数表达式中可以用φ、×或d来表示其为约束项,如:F(A,B,C)=∑m(0,1,5,7)+∑mφ(4,6)。
2、约束项在函数化简时的处理
在约束项的函数化简时,约束项一般具有一种特殊的地位,其既可以看作0又可以看作1来处理,取决于化简有利原则,即作为1处理对化简有利则看作1处理,否则看作0处理。
3、带约束条件的函数化简
带约束条件的函数化简方法与不带约束条件的方法相同,仅对在处于约束项时加以考虑就是了。
1.画出函数对应的卡诺图,将约束项对应的小方格用φ、×或d填上;
2.按2的整数次方个为1的小方格圈成一个矩形,如果在圈时约束项当作1来圈时圈得可以更大些,则当作1来处理,否则当0处理,对于来被圈个的约束项一律看作0。
3.写出化简的表达式。
例 化简函数F(A,B,C,D)=∑m(5,6,7,8,9)+∑mφ(10,11,12,13,14,15)
上图中a中我们在化简时将其约束项全部看作为1来处理的,而b图中将约束项看作为0了,从上图的化简不难看出,当奖约束项看成为1时,对化简有利。但不是在一个卡诺图上约束项全部看成1或全部看成0,而是根据化简有利的原则,哪一个约束项为1化简有利就看成1处理。
|
|
|