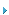摘 要: 针对装有可调变比变压器和补偿电容的电力系统,提出了一种在电力市场模式下进行分段计算的无功优化算法。该方法采用了遗传算法和Alopex方法相结合,能够在满足当日内变压器分接头和补偿电容动作次数约束和电压合格率的条件下,有效地降低网损。通过对IEEE14节点的计算结果表明,此方法是可行的。
关键词: 电力系统;无功优化;遗传算法;Alopex方法
引言
无功功率和电压幅值有密切的关系,它直接影响到电能的质量。当系统中的无功不足时,会导致电压水平下降,系统网损增加,稳定性下降,用户部分用电设备工作不正常等一系列问题[1]。因此在现代电力系统中要特别重视无功功率的配置和平衡,实现电力系统的无功优化。
电力系统无功优化是指在满足系统各种运行约束的条件下,通过优化计算确定发电机的端电压、有载调压变压器的分接头档位和无功补偿设备的投入容量等,以达到系统有功网损最小等目标[2,3,4]。在传统的电力系统无功优化的数学模型中,往往只考虑了有功功率的价格,以系统有功网损最小作为目标函数[5]。而在电力市场条件下,实行的是厂网分开,竞价上网,电厂和电网已经分属于不同的电力公司,各个公司都追求各自的经济利益最大化。而无功功率本身是无价的,它是生产有功功率的副产品,对于发电厂来说不能带来经济效益,这就不利于发电厂发出系统需要的无功功率。因此这种传统的无功优化模型已不能适应电力市场中的实际情况。为了使发电厂发出所需的无功功率,就必须给无功功率一定的价格,给发电厂一定的经济补偿以提高发电厂发出无功的积极性。因此,本文提出的无功优化数学模型不仅考虑了系统有功损耗费用还考虑了发电机发出的无功功率的费用。
本文在满足一天内变压器分接头和补偿电容动作次数约束和电压合格率的条件下,结合电力市场的相关情况提出了对一天内负荷进行无功优化的分段算法,并采用了遗传算法和Alopex方法相结合的算法进行计算。
1无功优化的数学模型
因为要通过调整无功功率在系统的分布来达到降低损耗的目标,而且在一般情况下,有功和无功负荷曲线的变化趋势是基本一致的,因此本文采用了对无功负荷曲线进行分段的方法。
通过负荷预测已知一天内无功负荷曲线的前提下,根据无功的负荷曲线(本文取为24点)和可调变压器分接头的允许动作次数对负荷曲线进行分段。具体方法如下。
因为要通过调整无功功率在系统的分布来达到降低损耗的目标,而且在一般情况下,有功和无功负荷曲线的变化趋势是基本一致的,因此本文采用了对无功负荷曲线进行分段的方法。
通过负荷预测已知一天内无功负荷曲线的前提下,根据无功的负荷曲线(本文取为24点)和可调变压器分接头的允许动作次数对负荷曲线进行分段。具体方法如下。

对于图1所示的负荷曲线,求出各时段相应的功率变化值 按照ΔQi由大到小的顺序排序,取最大的nl-1个值对应的时间点作为分段的边界,这样就将负荷曲线分为了nl段。
按照ΔQi由大到小的顺序排序,取最大的nl-1个值对应的时间点作为分段的边界,这样就将负荷曲线分为了nl段。
其中nl为一天内变压器分接头允许动作的次数。
1.1目标函数
发电机运行时要受到发电容量的限制。当发电机在发出无功功率时,在某些情况下其有无功出力的极限比没有无功出力情况下的极限值要小,从而造成发电厂隐性的经济损失,此时即使该有功功率无需发出,也会影响到这部分有功功率可作为旋转备用的相应利润,这在经济学上一般称为无功功率的机会成本(opportunity cost)。发电机的运行状态可以分为以下三种情况:
1) 当发电机的无功出力在0到QGN范围时不影响发电机发出有功,它完全是发电机的附带能力。这时无功的价格可以是零或较接近零的一个小数。
2) 当发电机的无功出力大于QGN时电机增发的无功,是以少发有功换来的,这就影响了发电机发出有功的收入,相应的电网公司应该给以适当的经济补偿。所以这时的无功价格应该大于无功出力在0到QGN时的无功价格。
3) 当发电机进相运行时,发电机吸收系统中的感性无功。这不仅减少了发电机有功出力,而且造成发电机端部发热,加速了发电机绕组绝缘的老化,减少了发电机的运行寿命。因而影响电厂的当前利益和长期利益。在这种情况下,发电机吸收感性无功的价格应该大于2)中的无功价格。其中:QGN为发电机的额定无功出力。
因此每一分段的无功优化数学模型如下:
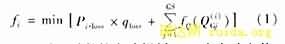
式中:Pi·loss为i时段的有功损耗,qloss为有功电价,GS为系统中发电机数, 为i时段第j台发电机的无功费用。
为i时段第j台发电机的无功费用。
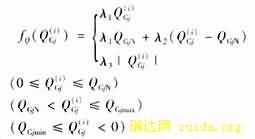
λ1,λ2,λ3为各运行状态下发电机的无功费用并且满足λ1<λ2<λ3。
本文所提出的一天无功优化数学模型如下:

其中:fi为每一分段的费用值,l为一天负荷曲线的分段数。
1.2约束条件
无功优化的约束条件可以分为等式约束和不等式约束:
等式约束:
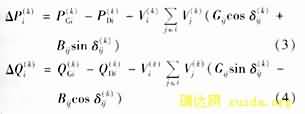

不等式约束:

式中:GS为系统中发电机数,mT为可调变压器数,NC为补偿电容数,NL为补偿电抗数,l为一天负荷曲线的分段数。
其中nl为一天内变压器分接头允许动作的次数。
1.1目标函数
发电机运行时要受到发电容量的限制。当发电机在发出无功功率时,在某些情况下其有无功出力的极限比没有无功出力情况下的极限值要小,从而造成发电厂隐性的经济损失,此时即使该有功功率无需发出,也会影响到这部分有功功率可作为旋转备用的相应利润,这在经济学上一般称为无功功率的机会成本(opportunity cost)。发电机的运行状态可以分为以下三种情况:
1) 当发电机的无功出力在0到QGN范围时不影响发电机发出有功,它完全是发电机的附带能力。这时无功的价格可以是零或较接近零的一个小数。
2) 当发电机的无功出力大于QGN时电机增发的无功,是以少发有功换来的,这就影响了发电机发出有功的收入,相应的电网公司应该给以适当的经济补偿。所以这时的无功价格应该大于无功出力在0到QGN时的无功价格。
3) 当发电机进相运行时,发电机吸收系统中的感性无功。这不仅减少了发电机有功出力,而且造成发电机端部发热,加速了发电机绕组绝缘的老化,减少了发电机的运行寿命。因而影响电厂的当前利益和长期利益。在这种情况下,发电机吸收感性无功的价格应该大于2)中的无功价格。其中:QGN为发电机的额定无功出力。
因此每一分段的无功优化数学模型如下:
式中:Pi·loss为i时段的有功损耗,qloss为有功电价,GS为系统中发电机数,
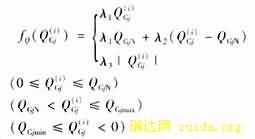
λ1,λ2,λ3为各运行状态下发电机的无功费用并且满足λ1<λ2<λ3。
本文所提出的一天无功优化数学模型如下:
其中:fi为每一分段的费用值,l为一天负荷曲线的分段数。
1.2约束条件
无功优化的约束条件可以分为等式约束和不等式约束:
等式约束:
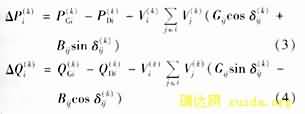

不等式约束:

式中:GS为系统中发电机数,mT为可调变压器数,NC为补偿电容数,NL为补偿电抗数,l为一天负荷曲线的分段数。
2无功优化计算方法
电力系统无功优化是指系统在一定运行方式下,要求解满足各种约束条件、达到有功网损最小等预定目标的优化问题。它涉及到无功补偿容量的确定、变压器分接头的调节和发电机端电压的选择以及它们的配合等,是一个离散的多约束的非线性规划问题。非线性规划法存在着不适于离散变量的缺陷。同时,由于局部收敛而常常收敛到局部最优点。遗传算法可较好地对离散变量进行处理且具有全局收敛性,但计算时间较长。因此本文采用把遗传算法和Alopex方法相结合的算法。它发挥了遗传算法全局寻优的能力,又具有一定的方向性,提高了计算速度。
2.1Alopex方法
Alopex方法是一种启发性和随机并行的优化算法。它将启发性与随机性相结合,使其本身既具有随机性,能够跳出局部最优值做到全局搜索,又具有启发性,能够从前次自变量的变化对目标函数产生的影响中受到启发,使算法尽量向最优解方向前进。并在过程控制参数“温度”的作用下,逐渐由随机优化变成确定方向搜索,最终收敛到全局最优解。
对于实际优化问题,可归结为求一个目标函数F(x1,x2,…,xn)的全局极值问题,其中x1,x2,…,xn为待确定的自变量,Alopex方法如下:
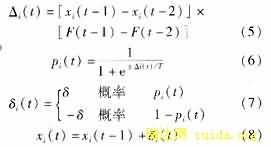
式中F(x1,x2,…,xn)为目标函数,xi(t)为F中第i个自变量在t时刻的取值,δi(t)为t时刻自变量xi(t)随机行走的步长, pi(t)为t时刻向增加δ方向行走的概率。式(6)中的正负号选取与实际问题有关,正号使目标极小化,负号使目标极大化,F(t-1),F(t-2)即F(x1(t-1),x2(t-1),…,xn(t-1))和F(x1(t-2),x2(t-2),…,xn(t-2))表示F在(t-1),(t-2)时刻的取值。
2.2遗传算法的改进
由于简单遗传算法存在着收敛速度慢,容易产生局部收敛等问题。因此本文对简单遗传算法做了以下的改进:
1) 选择:本文的选择策略如下:在某次代中,将父代和子代所有个体的适应值求平均值,产生一个随机数rnd,对于那些适应值高于平均值的个体,将其与选择概率Ps进行比较,若rnd≤Ps则选择该个体,否则淘汰该个体。对于那些适应值低于平均值的个体,若rnd≥Ps则选择该个体,否则淘汰该个体。这样不仅保留了群体中那些适应值较高的个体,以利于搜寻最优值使迭代收敛,而且保留了一些“较差的”值,又保证了个体在解空间中的分散性,在一定程度上避免了“早熟”现象。由于采用的是竞争的选择策略,所以若在某代群体中有个别个体的适应值大大高于其他个体,该个体也只会入选一次,这种方法使每个个体入选的概率与适应值的大小不直接成比例,在一定程度上避免了“家族优势”。在本文中,对于该代中的最优个体不进行上述操作直接进入下一代。
2) 杂交和变异:对于杂交和变异采用了模板杂交和变异的方法,即首先随机建立一个与个体码串长度相同的二进制码串作为模板,然后依据模板上相应位置是0还是1确定是否进行杂交和变异。这样做可以使基因中的各个位得到同样的杂交和变异的机会,充分发挥每个控制变量的作用,扩大搜索范围以找到最优解。
2.3遗传算法与Alopex方法的结合
遗传算法与Alopex方法相结合的具体做法为:
在杂交算子的后面加上Alopex方法,由于Alopex方法能在产生子代的同时随机产生一定的“噪声”,使子代与父代相比有一定的差异,这样不但会使种群具有一定的多样性,也使得算法有机会跳出局部极小值,收敛到全局最优,并可以在一定程度上加快收敛速度。此外Alopex算法在搜索过程中利用了前一次自变量及其函数值的变化信息,即方向信息,将有利于缩短搜索时间,而且其“噪声”随着收敛过程的进行逐步减少也有利于优化向全局最优前进。
在未改进的Alopex方法中,自变量正向变化和反向变化的步长相等。但是在实际优化中,自变量按正方向变化时步长应该小一些,以免由于步长过大而错过最优值。而自变量向反方向变化时步长应该大一些,因为自变量向反方向变化就是为了能使目标函数摆脱局部最优值。因此,本文对Alopex方法作了一些改进,即采用了变化的步长。本文中步长δ取为 其中a,γ为常数,可根据不同的优化问题来选择合适的值。当自变量按正方向变化时步长应该小一些(0<γ≤1),以免由于步长过大而错过最优值。而当自变量向反方向变化时步长应该大一些(γ>1),使目标函数能够摆脱局部最优值。而且随着迭代次数的增加,步长δ越来越小也有利于收敛到最优值。
其中a,γ为常数,可根据不同的优化问题来选择合适的值。当自变量按正方向变化时步长应该小一些(0<γ≤1),以免由于步长过大而错过最优值。而当自变量向反方向变化时步长应该大一些(γ>1),使目标函数能够摆脱局部最优值。而且随着迭代次数的增加,步长δ越来越小也有利于收敛到最优值。
电力系统无功优化是指系统在一定运行方式下,要求解满足各种约束条件、达到有功网损最小等预定目标的优化问题。它涉及到无功补偿容量的确定、变压器分接头的调节和发电机端电压的选择以及它们的配合等,是一个离散的多约束的非线性规划问题。非线性规划法存在着不适于离散变量的缺陷。同时,由于局部收敛而常常收敛到局部最优点。遗传算法可较好地对离散变量进行处理且具有全局收敛性,但计算时间较长。因此本文采用把遗传算法和Alopex方法相结合的算法。它发挥了遗传算法全局寻优的能力,又具有一定的方向性,提高了计算速度。
2.1Alopex方法
Alopex方法是一种启发性和随机并行的优化算法。它将启发性与随机性相结合,使其本身既具有随机性,能够跳出局部最优值做到全局搜索,又具有启发性,能够从前次自变量的变化对目标函数产生的影响中受到启发,使算法尽量向最优解方向前进。并在过程控制参数“温度”的作用下,逐渐由随机优化变成确定方向搜索,最终收敛到全局最优解。
对于实际优化问题,可归结为求一个目标函数F(x1,x2,…,xn)的全局极值问题,其中x1,x2,…,xn为待确定的自变量,Alopex方法如下:
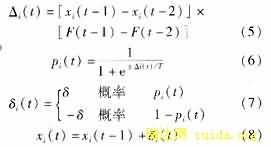
式中F(x1,x2,…,xn)为目标函数,xi(t)为F中第i个自变量在t时刻的取值,δi(t)为t时刻自变量xi(t)随机行走的步长, pi(t)为t时刻向增加δ方向行走的概率。式(6)中的正负号选取与实际问题有关,正号使目标极小化,负号使目标极大化,F(t-1),F(t-2)即F(x1(t-1),x2(t-1),…,xn(t-1))和F(x1(t-2),x2(t-2),…,xn(t-2))表示F在(t-1),(t-2)时刻的取值。
2.2遗传算法的改进
由于简单遗传算法存在着收敛速度慢,容易产生局部收敛等问题。因此本文对简单遗传算法做了以下的改进:
1) 选择:本文的选择策略如下:在某次代中,将父代和子代所有个体的适应值求平均值,产生一个随机数rnd,对于那些适应值高于平均值的个体,将其与选择概率Ps进行比较,若rnd≤Ps则选择该个体,否则淘汰该个体。对于那些适应值低于平均值的个体,若rnd≥Ps则选择该个体,否则淘汰该个体。这样不仅保留了群体中那些适应值较高的个体,以利于搜寻最优值使迭代收敛,而且保留了一些“较差的”值,又保证了个体在解空间中的分散性,在一定程度上避免了“早熟”现象。由于采用的是竞争的选择策略,所以若在某代群体中有个别个体的适应值大大高于其他个体,该个体也只会入选一次,这种方法使每个个体入选的概率与适应值的大小不直接成比例,在一定程度上避免了“家族优势”。在本文中,对于该代中的最优个体不进行上述操作直接进入下一代。
2) 杂交和变异:对于杂交和变异采用了模板杂交和变异的方法,即首先随机建立一个与个体码串长度相同的二进制码串作为模板,然后依据模板上相应位置是0还是1确定是否进行杂交和变异。这样做可以使基因中的各个位得到同样的杂交和变异的机会,充分发挥每个控制变量的作用,扩大搜索范围以找到最优解。
2.3遗传算法与Alopex方法的结合
遗传算法与Alopex方法相结合的具体做法为:
在杂交算子的后面加上Alopex方法,由于Alopex方法能在产生子代的同时随机产生一定的“噪声”,使子代与父代相比有一定的差异,这样不但会使种群具有一定的多样性,也使得算法有机会跳出局部极小值,收敛到全局最优,并可以在一定程度上加快收敛速度。此外Alopex算法在搜索过程中利用了前一次自变量及其函数值的变化信息,即方向信息,将有利于缩短搜索时间,而且其“噪声”随着收敛过程的进行逐步减少也有利于优化向全局最优前进。
在未改进的Alopex方法中,自变量正向变化和反向变化的步长相等。但是在实际优化中,自变量按正方向变化时步长应该小一些,以免由于步长过大而错过最优值。而自变量向反方向变化时步长应该大一些,因为自变量向反方向变化就是为了能使目标函数摆脱局部最优值。因此,本文对Alopex方法作了一些改进,即采用了变化的步长。本文中步长δ取为
3计算步骤
1) 根据有功、无功负荷曲线和可调变压器分接头动作次数的限制,把负荷曲线划分成几个大时段。
2) 在每一个分段中,选择一个接近于该段平均负荷的典型负荷点,对该典型负荷点进行无功优化,得到相应的变压器分接头档位和补偿的投切组数。记下前N个最优解。
3) 对该段中其余的负荷点,将其变比固定为所得的最优解的变比,然后进行优化(即只进行发电机端电压和补偿的优化)。
4) 计算各负荷点的有功网损之和,在N个最优解中找出费用之和最小的解作为该段的优化解。
5) 对每一分段都进行上述计算,全天优化完毕后,计算平均的电压合格率
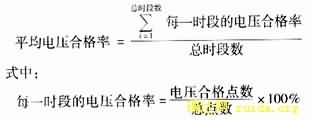
6) 若平均电压合格率满足要求,则优化结束。输出各时段的变压器分接头档位和补偿的投入组数。若不满足要求,则将电压合格率最低的一个分段再划分为两个时段重新进行2)、3)、4)、5)步的计算。
1) 根据有功、无功负荷曲线和可调变压器分接头动作次数的限制,把负荷曲线划分成几个大时段。
2) 在每一个分段中,选择一个接近于该段平均负荷的典型负荷点,对该典型负荷点进行无功优化,得到相应的变压器分接头档位和补偿的投切组数。记下前N个最优解。
3) 对该段中其余的负荷点,将其变比固定为所得的最优解的变比,然后进行优化(即只进行发电机端电压和补偿的优化)。
4) 计算各负荷点的有功网损之和,在N个最优解中找出费用之和最小的解作为该段的优化解。
5) 对每一分段都进行上述计算,全天优化完毕后,计算平均的电压合格率

6) 若平均电压合格率满足要求,则优化结束。输出各时段的变压器分接头档位和补偿的投入组数。若不满足要求,则将电压合格率最低的一个分段再划分为两个时段重新进行2)、3)、4)、5)步的计算。
4算例
采用本文提出的算法对IEEE-14Bus系统进行了计算。一天负荷曲线如图1所示,电源节点的电压幅值设为0.90到1.10,负荷节点的电压幅值设为0.95到1.05,变压器变比为0.9到1.1,档距为0.0125,一天动作次数限制为6次。在补偿节点处有5组电容器和5组电抗器,每组标么值为0.1。根据负荷曲线取分段数为3,无功优化后的结果为表1所示。
采用本文提出的算法对IEEE-14Bus系统进行了计算。一天负荷曲线如图1所示,电源节点的电压幅值设为0.90到1.10,负荷节点的电压幅值设为0.95到1.05,变压器变比为0.9到1.1,档距为0.0125,一天动作次数限制为6次。在补偿节点处有5组电容器和5组电抗器,每组标么值为0.1。根据负荷曲线取分段数为3,无功优化后的结果为表1所示。

从结果可知,变压器1总变化次数为3,变压器2总变化次数为2,变压器3总变化次数为3,平均电压合格率为100%,均满足要求。
5结论
本文在满足一天内变压器分接头和补偿电容动作次数约束和电压合格率的条件下,提出了对一天内负荷进行无功优化的分段算法,其中也兼顾考虑了电力市场的相关约束情况。并采用了遗传算法和Alopex方法相结合的算法进行计算。通过对算例的计算,结果说明本文提出的方法是可行的。
本文在满足一天内变压器分接头和补偿电容动作次数约束和电压合格率的条件下,提出了对一天内负荷进行无功优化的分段算法,其中也兼顾考虑了电力市场的相关约束情况。并采用了遗传算法和Alopex方法相结合的算法进行计算。通过对算例的计算,结果说明本文提出的方法是可行的。
参考文献
[1] 何仰赞, 温增银, 汪馥瑛,等(HE Yangzan, WEN Zengyin, WANG Fuying, etal).电力系统分析(Analysis of Power System)[M]. 武汉:华中理工大学出版社(Wuhan: Huazhong University of Technology Press), 1996.
[2]Bridenbaugh C J, DiMascio D A, Aquila R D.Voltage Control Improvement Through Capacitor and Transformer Tap Optimization[J]. IEEE Trans on Power Systems, 1992,7(1): 222-227.
[3]Shuster M D .A Survey of Attitude Representations[J] .Journal of the Astronautical Science ,1993,43.
[4]马晋涛, Lai LL, 杨以涵(MA Jintao , Lai L L ,YANG Yihan ).遗传算法在电力系统无功优化中的应用(Application of Genetic Algorithm in Reactive Power Optimization)[J]. 中国电机工程学报(Proceedings of the CSEE), 1995,15(5):347-353.
[5]谭伦农,张保会,段建东(TAN Lunnong, ZHANG Baohui, DUAN Jiandong). 电力市场下的一种无功优化方法(Method of Reactive Power Optimization in Power Market)[J]. 西安交通大学学报(Journal of Xi′an Jiaotong Univertity), 2002,36(10):996-999.
[6]Lu F C, Hsu Y Y. Reactive Power/ Voltage Control in a Distribution Substation Using Dynamic Programming[J]. IEE Proceedings,Part C,1995,142(6).
[7]许文超,郭伟(XU Wenchao,GUO Wei).电力系统无功优化的模型及其算法综述(Summarization of Reactive Power Optimization Model and Algorithm in Electric Power System)[J].电力系统及其自动化学报(Proceedings of the EPSA),2003,15(1):100-104.
[8]任晓娟,邓佑满,赵长城(REN Xiaojuan, DENG Youman,ZHAO Changcheng) .高中压配电网动态无功算法的研究(Study on the Algorithm for Dynamic Reactive Power Optimization of Distribution System)[J].中国电机工程学报(Proceedings of the CSEE),2003,23(1):31-36
[9]邓佑满(DENG Youman). 配电网络优化的理论与算法(The Optimum Theory and Algorithm of Distribution Network)[M]. 北京:清华大学出版社(Beijing: Tsinghua University Press),1994.
[2]Bridenbaugh C J, DiMascio D A, Aquila R D.Voltage Control Improvement Through Capacitor and Transformer Tap Optimization[J]. IEEE Trans on Power Systems, 1992,7(1): 222-227.
[3]Shuster M D .A Survey of Attitude Representations[J] .Journal of the Astronautical Science ,1993,43.
[4]马晋涛, Lai LL, 杨以涵(MA Jintao , Lai L L ,YANG Yihan ).遗传算法在电力系统无功优化中的应用(Application of Genetic Algorithm in Reactive Power Optimization)[J]. 中国电机工程学报(Proceedings of the CSEE), 1995,15(5):347-353.
[5]谭伦农,张保会,段建东(TAN Lunnong, ZHANG Baohui, DUAN Jiandong). 电力市场下的一种无功优化方法(Method of Reactive Power Optimization in Power Market)[J]. 西安交通大学学报(Journal of Xi′an Jiaotong Univertity), 2002,36(10):996-999.
[6]Lu F C, Hsu Y Y. Reactive Power/ Voltage Control in a Distribution Substation Using Dynamic Programming[J]. IEE Proceedings,Part C,1995,142(6).
[7]许文超,郭伟(XU Wenchao,GUO Wei).电力系统无功优化的模型及其算法综述(Summarization of Reactive Power Optimization Model and Algorithm in Electric Power System)[J].电力系统及其自动化学报(Proceedings of the EPSA),2003,15(1):100-104.
[8]任晓娟,邓佑满,赵长城(REN Xiaojuan, DENG Youman,ZHAO Changcheng) .高中压配电网动态无功算法的研究(Study on the Algorithm for Dynamic Reactive Power Optimization of Distribution System)[J].中国电机工程学报(Proceedings of the CSEE),2003,23(1):31-36
[9]邓佑满(DENG Youman). 配电网络优化的理论与算法(The Optimum Theory and Algorithm of Distribution Network)[M]. 北京:清华大学出版社(Beijing: Tsinghua University Press),1994.