摘  要: 本文将神经网络控制应用于PWM整流器中，改善了控制效果。仿真与实验验证了控制方案的可行性和优越性。

关键词：神经网络  整流器  功率因数校正  系统实验

Application of Neural Networks to PWM Rectifier Control

Li shunyuan   Shun xiaofeng  Meiqiang  Wu weiyang

Yanshan University of Technology  066004  Qinhuangdao

Abstract: In this pater, The neural-network control is selected as the PWM rectifier control strategy,  Improved the performance of the system. The feasibility and advantage of the control scheme is verified by simulation and experiment.

Keyword：Neural Network  Rectifier  Power factor correction  System experiment

1  引  言

   神经网络控制作为一种极有潜力的控制手段吸引了众多学者的研究[1]，因其本身具有并行处理能力、自学习能力、容错能力，很适合于处理非线性系统的控制问题[2]。而电力电子系统属于比较严重的非线性系统, 在单位功率因数整髌髦校缌骺刂票旧硎且恢趾芮康姆窍咝钥刂疲车闹突返缌骺刂平虾玫奶逑至苏庖坏鉡3]。它也因此取得了较好的鲁棒性和快速的电流响应.。但是它开关频率不固定，本文在滞环控制的基础上用先离线训练了一个神经网络控制器代替滞环控制器,这种控制方法保持了滞环电流控制鲁棒性好，电流响应快的优点，同时可以限制器件的最高开关频率。

2  控制系统的工作原理

高功率因数PWM整流器的结构如图１所示，其工作原理见文献[4]

图1  三相电压源变流器主电路

用神经网络来控制的整流器的控制原理

图如图2所示（单相等效电路）。

图2  系统控制框图

参考电压Uref同输出电压Uo的差值经PI调节后，取其为电流峰值参考，再分别与对应相的同步信号相乘，得到内环电流的参考

信号im*，再与实际相电流im相比较得到电流误差信号Δi=im*-im,，电流误差信号再输入神经网络控制器，神经网络的输出即为开关信号。其导师信号见表１

本文中的神经网络拓扑结构如图３所示（包括输入层），为三层前向神经网络，学习算法是误差反向传播方法（BP算法）。

节点的作用函数采用Sigmoid函数 O 式中O 是第r步迭代时第k层第 i个神经元节点对于第h个样本输入时的输出， 为第r步时第k层第 i个神经元节点对于第h个样本输入时所接收到的上一层（第k-1层）的输入总和

表1  导师信号

, 为第r步迭代时第k-1层第j个神经元节点对于第k层第i个神经元的权系数.， 为第r步迭代时第k层第i节点的阀值，使用平方型误差函数 ，以及H个样本总误差 ，式中 为第h个样本输入时，输出层第i个神经元节点的期望输出。采用使用最为广泛的BP算法，网络的学习表达式如下：

          (1)

     (2)

式中   μ为为学习步长

对于输出层（在本文中为第3层）

对于中间层有

图3  神经网络控制器

上面是最基础的BP训练学习算法，在它的基础上可以有变学习步长或带动量项系数的BP算法。

采用批处理的学习方法，依表一的学习规则用matlab进行离线训练得到网络的结构为（3，4，3），通过多次反复训练，取系统的训练误差为1%100，同时考虑到神经网络控制器用定点DSPTMSF240实现时数值范围和数值精度的矛盾，决定取网络各层的权值和各个神经元的阀值如下：

再利用MATLAB中的Simulik环境搭出神经网络控制器作为一个子系统置于整个系统中。来仿真验证控制方案的可行性。

3  仿  真

MATLAB是基于系统数学模型的功能强大的仿真工具，本三相变流器的数学模型取图1所示主回路在三相静止坐标系下的数学模型即可[5]，如下所示：

                  (3 )

其中，

fk为三相整流桥的开关函数

fk =

其中，k=1,2,3

外面的电压环用传统的PI调节器，内环电流环采用上面权值与阀值的(3,4,3)结构的神经网络控制器。

电路参数如下：

输入电压：Ua=Ub=Uc=50V，直流输出电压Uo=200V，交流侧电感：L=6Mh

直流侧输出电容：C=3000UF，直流负载电阻：R=40Ω，采样频率为10K

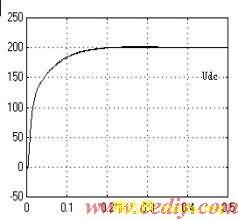图4 直流电压响应波形

图 4  电压响应仿真波形

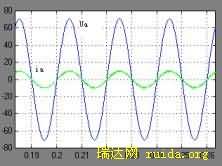图5  A相电压和电流仿真波形

从图4,5可以看出系统的响应时间约为0.15S,具有较快的响应速度和单位功率因数。

4  系统实验

 本文用DSP软件实现神经网络控制器用于三相高功率因数变流器的控制中，实现了系统的实时控制，限制了最高开关频率为5K，实验波形如图6,7所示。图7中幅值大的为相电压波形，幅值小的为电流波形i为4A/格。可见，在神经网络控制器的作用下系统实现了单位功率因数。                

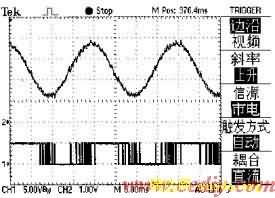    图6  A相开关信号和A相电流波形

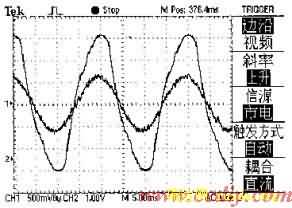                                                 图7  A相电压与电流实验波形

5  结  论

本文提出了一种基于神经网络控制的PWM整流器的控制方案，能实现单位功率因数，且具有快速的系统响应。神经网络控制应用于电力电子这种非线性系统中是一种新颖的、很有前途的控制策略。

参考文献：

[1] 袁再任. 人工神经元网络及其应用.  清华大学出版社,  1999

[2] 吕征宇, 钱兆明. 并联有源电力滤波器的神经网络预测控制,  中国电机工程学报，1999，19（12）

[3] F.De Winter,Y.Xiao.l  “A High Power AC/DC Current Source Converter with Sinusiodal Input Current and Unity Power Factor”,IPEMC’97  91-95

[4]J.Dixon,S.Tepper,L.Moran.Practical

Evaluation of different Modulation Techniques for Current-controlled Voltage Source Inverters IEE Proc.Electr.Power Appl. 1996,143(4):301~306

[5] W.R.Song. Analysis of an Ac-to-Dc Voltage Source Converter Using PWM with Phase and Amplitude Control.IEEE Trans On IA, 1991, 2(27):355-363

作者简介：

黎顺元  男  1976年生，硕士，助教，研究兴趣为电力电子技术，微处理器技术.智能控制。

孙孝峰  男  1970年生，博士生，讲师，研究兴趣为电力电子技术，计算机控制技术。

梅  强  男  1975年生，硕士，助教，研究兴趣为电力电子技术。

邬伟扬  男  1940年生，教授，博士生导师。主要研究方向为大功率牵引传动. 高功率因数。