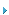．引言

高频感应加热电源必须对加热装置的输出功率和工作频率加以控制，控制效果的好坏直接影响到加热工件的表明质量和成本。因此一个实用的加热装置应该能在较大的功率范围内进行精确的调节。但在加热过程中，由于温度的影响以及电网的干扰等都会造成负载的等效参数发生变化，单闭环的功率控制器往往会造成电源主回路谐振频率变化，这样电源的输出功率会不稳定，常会致使逆变器件过压损坏。针对这种情况，本文提出了一种双闭环控制结构和模糊控制方法，使得负载变化时保持电磁炉的输出功率稳定。实际结果表明了设计的有效性和可靠性[1]

2.电源的控制系统结构

在感应加热电源单闭环的控制系统中，当功率受到扰动增大时，由于负反馈的作用，使得逆变器件的触发脉冲变窄，输出功率下降。这样一个单闭环结构可以保证在单片机输出PWM固定而且负载等效参数恒定的情况下，感应加热电源的输出功率稳定在某一工作点(功率)上。但是随着温度的变化，输出功率会稳定在一个新的工作点上。针对这这种情况，在上述电路的基础上，增加了一个闭环控制，如图1所示。这样原电路变成了一个双闭环结构。当负载变化时，由外环检测出来，在单片机内部采用模糊PID控制策略，调节输出PWM的占空比，以保证负载变化时，输出功率的恒定。

3．模糊控制器的设计

在工业过程控制中，广泛使用常规PID控制器，原因在于常规PID控制原理简单，容易实现，稳态无静差。因此，长期以来广泛应用于工业过程控制，并取得了良好的控制效果。但是，常规PID控制器存在着参数调节需要一定过程，最优参数选取有一定麻烦以及当系统中一些参数发生变化时，控制器的参数就会无法有效地对系统进行控制等缺点。由于在实际中，大多数工业过程都不同程度地存在非线性、参数时变性和模型不确定性，因而常规PID控制无法实现对这样的过程的精确控制。模糊控制对数学模型的依赖性弱，不需要建立过程的精确数学模型。由于模糊参数自适应PID控制器是以过程控制的知识为基础的，以模糊规则所组成的知识库，用模糊控制规则和推理，确定PID控制器的参数，并能够进行实时联机修正参数，使控制器适应被控对象的任何参数变化。因此本文尝试用模糊PID这一控制算法。

下面是模糊控制器的设计步骤[2]：

3．1 常规PID控制器算法

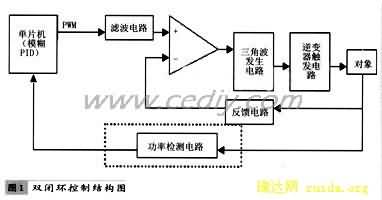
PlD控制器的数学模型可用下式表示：

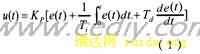或写成传递函数形式

其中，u(t)为控制器输出；e(t)为控制器偏差输入；Kp、Ti和Td分别为控制器的比例系数、积分时间常数和微分时间常数。

在离散系统中，PID控制器采用差分方程表示为：

(3)

式中：k一采样序号，k=0，1， 2， …；

u(k)-第k次采样时刻的计算机输出值；

e(k)-第k次采样时刻输入偏差值；

e(k-1)-第k-1次采样时刻输入偏差值；

3．2 确定语言变量和隶属函数

为了能使模糊控制规则可以对PID参数进行推理，故而需要对PID控制器的一些参数作一定处理，并且还有利于进行参数的实际修正[3]。

考虑上式表达的常规PID控制器。在式中，T是采样周期，e(k)，e(k-1)是输入量，故它们都是已知量；则未知量，即参数是KP、KI和KD，它们是需要进行定的。在一般系统中，KP、KI和KD使用扩充临界比例度法或者扩充响应曲线等实用工程方法整定，这些工程方法都要对被控对象进行现象实际测定之后，才能确定KP、KI和KD等参数。

为了寻找可以实时推理出恰当的PlD参数的模糊控制规则，对有关参数作一些规定。假设KP的范围为[KPmin，KPmax]，KD的范围为[KDmin，KDmax]，则通过下面的线性变换使KP、KD的范围归一化到[0，l ]：

在PID控制器中，还存在积分系数KI。由于在模糊参数PID控制系统中，将会根据系统的偏差e(k),偏差变化率e(k)的情况去确定所有PID参数，因此，积分时间常数可以根据微分时间常数确定，即T_i=αT_d

由于积分系数KI为从而可得：

同时，因为有KD=KpTd,故有

由式（3－6）和（3－7）可得：

很明显，如果能确定K’P、K’D和α，那么，就可以十分容易求得PID系统的参数K_P、K_I和K_D：

因此，选用K’P、K’D和α作为模糊系统的输出语言变量。

3．3 确定各输入、输出变量的变化范围

在模糊控制规则中，e(k)和e c(k)的论域均为(一6，一5，一4，一3，一2，一1，O，1，2，3，4，5，6)，它们的语言变量值取“负大”

(NB)， “负中”(NM)， “负小”

(N s)， “零”(z O)，“正小”

(PS)， “正中”(PM)，“正大”

(PB)共7个值。它们的隶属函数都是三角形，并且，每个值所取的范围宽度相等。它们的隶属函数如图2所示。

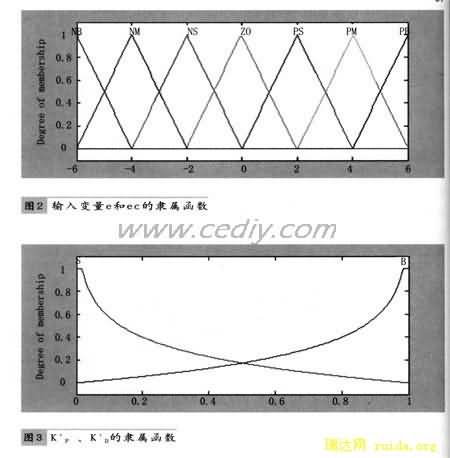
修正系数K’P、K’D是用于求取比例系数K，和微分系数K。的；它们是在闭区间[0，1]中取值的；并且其语言变量值取“大”(B)和“小”(s)这两种。这两个语言变量值的隶属函数如图3所示。其中，语言变量值“大”(B)的隶属函数μB用下式表示：；语言变量值“小”(S)的隶属函数μS表达式如下：

α的论域为{1，2，3，5，6}，并取4种语言变量值“小”(S)、 “中小”(M S)、 “中”(M)、 “大”(B)。隶属函数为梯形，如图3—6所示。

3．4 模糊控制规则的产生

模糊参数PID控制系统是在一般的PID控制系统的基础上，加上一个模糊控制规则环节。模糊控制规则环节是为了根据系统实时状态调节PID的参数而设置的。在实际的控制中，用模糊规则和推理去实时校正PID参数，从而适应被控对象参数变化。因此，模糊自适应PI D控制系统的关键在于模糊控制规则对PID参数的调节机理及过程。

根据参数KP、KI和KD对系统输出特性的影响情况，可归纳出在一般情况下，对于不同的e和e c，被控过程对参数K’P、K’D和α的调节规则。

通常，一个典型的系统阶跃响应曲线如图5所示。

1)系统启动瞬间，a点附近，y ≈ 0，e最大，为了加快系统的响应速度，并防止因e的瞬间变大可能引起的微分溢出，应取较大的KP，较小的KD和较大的KI，写成语言规则为：

if e i s PB and ec is ZO then K’P i s B， K’D i s S， α i s B

2)在过程中期，b点附近，e很小，为了使系统响应的超调减小和保证一定的响应速度，应取较小的KP，较大的KD和较小的KI，写成语言规则即为：

if e i s PB and ec i s ZO thenI；P i s S， K’D i s B， αi s S

3)c点附近，e数值较大，ec数值很小，情况同a点；

4)d点附近，e数值很小，ec数值较大，情况同b点。

通过以上分析，从而得到了e(k)和e(k)在不同情况时，PID控制器的有关参数K’P、K’D和α的模糊控制规则。如表1、2、3。

模糊控制表通过查询将当前时刻模糊控制器的输入变量量化，值(误差，误差变化量化值)所对应的控制输出值作为模糊逻辑控制器的最终输出，从而达到快速实时控制。模糊控制规则表必须对所有输入语言变量量化后的各种组合通过模糊逻辑推理的一套方法离线计算出每一个状态的模糊控制器输出，最终生成一张模糊控制表。

4．结论

实际运行结果表明，模糊PID控制比常规PID控制具有良好的动态性能，如上升时间、调节时间都比较短，而且无超调。本文使用的模糊PID方法控制效果好、易于实现，便于工程应用，与常规PID控制相比，不仅对被控参数变化适应能力强，而且在对象模型结构发生较大改变的情况下也能获得较好的控制效果。