晶体二极管电路的分析方法

晶体二极管是由PN结加上引出线和管壳构成的，具有PN结的各种特性，通常有以下几种类型：

点接触型：结面积小，结电容小，适用于高频如几百兆赫工作， 但不能通过很大的电流，主要用于小 电流的整流和高频时的检波、混频等。

面接触型：结面积大，结电容大，能通过较大的电流但只能在
低频下工作。一般在100KHz以下用作整流器件。

硅平面型：结面积较大的，可通过较大电流，适用大功率整流，结面积较小的，结电容较小，适用   于在数字电路中作开关管。
一、晶体二极管的模型：
        电路分析时，电路中的各个实际器件必须用其相应的模型来表示，即所谓的元件约束，常用其伏安特性来表示，但实际器件在各种不同条件下伏安特性是不同的，如二极管低频应用时可不考虑结电容效应，而在高频时结电容效 应不能忽略。工程上，常采用简化模型分析电路主要特性，而计算机辅助分析采用复杂模型以获得精确结果。 实际器件的模型一般有：数学模型、曲线和表格模型、电路模型等。
        1、晶体二极管的数学模型；P18—1式所示的指数特性为晶体二极管理想的 数学模型，实际器件的伏安特性一般用下式表示：
                                             V-Irs
                             I  = IS（enVT     —1）
 n为非理想化因子，其值与 I 有关，I 为正常值时，n≈1，I 过大或过小 时， n≈2，rs是与阻挡层相串接的电阻（中性区题电阻，引线电阻等） 如果进一步考虑击穿特性和非线性电容特性，模型更复杂，工程上常采 用理想的简化模型。                   
2、伏安特性曲线：可根据数学模型或实际测量获得二极管的 伏安特性曲线，如图P19所示。
3、简化电路模型：二极管的主要特性是其单向导电性，导通前（或外加反向电压）近似为开路，导通后近似为一线性电阻（导通电阻RD，其伏安特性曲线为如下两段直线近似，转折点为导通电压V(on)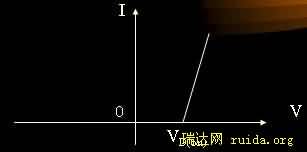

定义一种二极管为理想二极管，导通电压为零，导通电阻为零。
其电路符号为实际二极管电路符号为

实际二极管简化电路模型为：

4、小信号电路模型：实际器件交流和直流模型并不一样，交流模型中小信号和大信号、低频和高频模型也并不一样，线性电路中主要涉及低频小信号模型。如果加到二极管上的电压V是由直流电压VQ（决定二极管的静态工作点，用Q表示）和叠加其上的增量电压△V组成，则产生的电流 ：I = IQ +△I    一般来说叠加在Q点上的△V与△I 的关系是非线性的但若△V足够小（ ∣△V ∣<5.2mV) ，在△V 的变化范围内二极管伏安特性曲线近似为一段直线，如下图所示：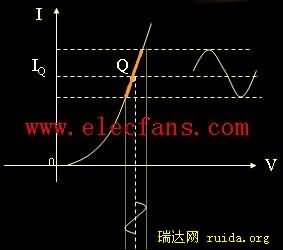

如上图一段红线所示，这时二极管小信号伏安特性近似为一个交流线性电阻rj ，其值为该直线段斜率的倒数：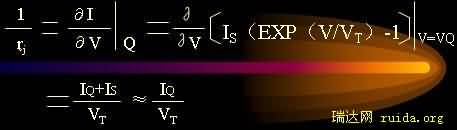

或rj = VT /  IQ通常称rj 为二极管的增量结电阻（肖特基电阻、交流小信号等效电阻）精确计算时还应考虑体电阻rs，高频时应考虑结电容Cj 。

二,晶体二极管电路分析方法：
        二极管在电路中，既应服从拓扑约束，又应服从元件约束，在不同的应用条件下，二极管采用不同的模型，分析方法也不同。
1、图解分析法：当二极管用伏安特性曲线模型时，可采用图解分析法。 先列出管外电路方程，该方程与伏安特性曲线的交点便是所需求的解。
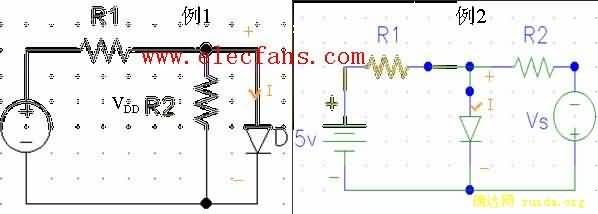
2、简化分析法：二极管采用简化电路模型，电路分析较简单，是最常用的分析方法，以上图所示电路为例：
例1：首先列出二极管管外电路方程，实际是将二极管两端（A、B两端）进行代文宁等效其开路电压VOC=VDD  R2 / R1  等效内阻R0= R1 // R2   从而   VAB=VOC—I R0    至此若用图解分析法
该直线与伏安特性曲线交点即所求解，若用简化分析法，将二极管等效为P25简化电路模型，则由于 VAB>0故VAB=I RD+VD（on） 该方程与上方程联立求的电路解。

例3：
已知两个二极管的VD（on）=0.7V，RD=100Ω，V1=100V，V2=25V,试求Vo随Vi 变化传输特性
解：由于 RD远小于外电阻R1、R2，VD（on）远小于外电源电压，故D1、D2近似为理想二极管。计算这一类型题目时，应先求出二极管导通和截止的条件，根据这个求输入输出关系，该题中D1导通条件是VA大于25V，D2导通条件是VA大于100V，因此当VA小于25V时，即 Vi小于25V ，D1、D2均不导通，输出Vo=25V ；当VA大于25V而小于100V时， D1导通， D2截止，此时VA大于25V相当于Vi大于25V，而输出电压

这时Vo随Vi线性增加，当Vo增至100V，即Vi=137. 5V时，VA=100V，D2导通，输出稳定在100V，与Vi无关。