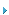摘  要：用数学模型精确地描述以及用实验验证DC/DC变换器的分岔和混沌现象一直具有较大的难度，从而导致以往理论研究结果的真实性受到质疑。为此该文以Buck DC/DC变换器为具体研究对象，提出其分岔和混沌分析精确离散建模方法，建立了它的精确离散数学模型。基于此模型进一步分析Buck DC/DC变换器分岔稳定性和混沌特性，改进了现有近似的模型的研究结果。同时文中还进行了丰富的实验研究，证实了该文精确数学模型的正确性，并实际展现了Buck DC/DC变换器从分岔至混沌演化的全过程。该文的研究方法也为其它DC/DC变换器的分岔和混沌现象提供了理论和实验基础，具有一般性意义。
    关键词：DC/DC变换器；分岔和混沌；模型和实验

1 引言
    Buck DC/DC变换器是1个典型的开关非线性系统，对其分岔和混沌现象的研究是目前电力电子技术的1个崭新的课题。由于Buck DC/DC工作模态的复杂性，它的分岔和混沌建模一直是一个困难的问题，现有的建模方法分为两类^[1-4]：① 是纯数值仿真方法；② 是近似离散模型分析方法。前者明显的缺点是无法得到解析结果，无法了解变换器内部参数间的相互关系，限制了进一步深入的研究。后者可以得到近似的解析结果和变换器内部参数间的大致相互关系，但一些有用的信息可能因为近似而被丢失，而对于非线性系统，参数的微小差异可能导致截然不同分析结果，使得出结论的真实性受到质疑^[5]。
    此外，Buck DC/DC变换器分岔和混沌现象的实验验证则是另一个困难的问题^[6-7]，大多数的研究都是停留在理论分析和仿真层面上，使得Buck DC/DC变换器分岔和混沌现象的实际控制和应用受到限制。
    因而，基于以上两个困难，开展对Buck DC/DC变换器精确离散建模和实验研究，并使其研究方法具有一般性，适合于其它DC/DC变换器分岔和混沌现象的分析。
2 Buck DC/DC变换器精确离散模型
    典型的Buck DC/DC变换器如图1所示。图中S为开关器件；V_D为续流二极管；i_L为电感L上流过的电流；v_o为负载两端输出的电压；v_o为电压反馈控制给定参考电压；E为输入电压；D是稳态工作时开关占空比，它等于S导通时间比上开关工作周期T； d_m是第m个开关周期占空比，当稳态工作时d_m=D；Dd_m是第m个开关周期占空比变化量；K是变换器比例反馈参数。

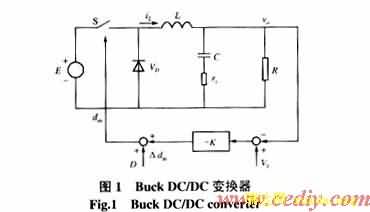
    当Buck DC/DC变换器工作在一般不连续模式时，在S一个开关周期内有3个工作模态：S导通，V_D不导通；S不导通，V_D导通；S、V_D均不导通。变换器工作在任一模态时，都可以列写它的状态方程，表示成矩阵形式如下

式中  N为系统具有N个不同工作模态，在Buck DC/DC变换器不连续模式时N=3；[t_i-1,t_i]为第i个工作模态的工作区间；x(t)为系统的状态变量组成的向量，一般为电感上电流和输出电压；A_i、B_i为系统在不同模态时的系数矩阵，它们只与模态有关，与时间无关；e(t)为系统输入电压函数，对于DC/DC变换器一般认为输入为稳定的直流电压，所以e(t)=E，E为常数。

式中 △t=t_i-t_i-1为每个开关模态的时间间隔，△t_i大小取决于变换器反馈控制规律的，参见图1。
    Buck DC/DC变换器的一般控制律为

式中 v_om是第m周期的输出电压（即反馈电压）。





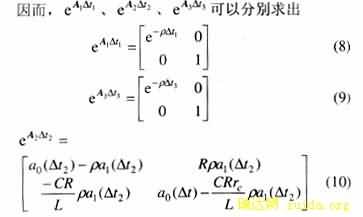
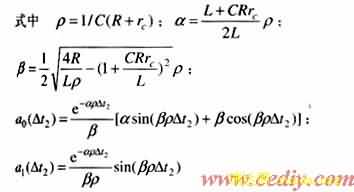
    将式(8)、(9)、(10)分别代入式(6)，就得到Buck DC/DC变换器的精确离散模型

3 Buck DC/DC变换器分岔稳定性分析
    离散系统的稳定性在稳定点X判别式为

稳定性判据可简化为

    考虑到当DC/DC变换器自身的主要参数确定后，它的稳定性直接取决于控制系统的设计。参见图1，K是Buck DC/DC变换器的比例反馈参数，因而它的大小直接影响到变换器的稳定性。取Buck DC/DC变换器参数如下：T=333.33μs；E=33V；V₀=25V；P=50W；L=208μH；C=222μF；R=12.5Ω；此外T/C（R+rc)=0.12。将参数代入式(11)，以反馈参数K为分岔变量，由式(13)可以得出与电压反馈参数K相关的稳定判别式如下

由上式可求得K的临界稳定值K_C=0.1335，当K<K_C，系统稳定运行，因此可知当K≥K_C系统将开始出现倍周期分岔，最终进入混沌状态。根据式(14)就可设计Buck DC/DC变换器的反馈系数，观察到它的分岔及混沌现象。
4 Buck DC/DC变换器分岔和混沌现象的实验研究
    Buck DC/DC变换器的分岔和混沌实验电路如图2。其反馈参数K通过调节R_f得到，具体的表

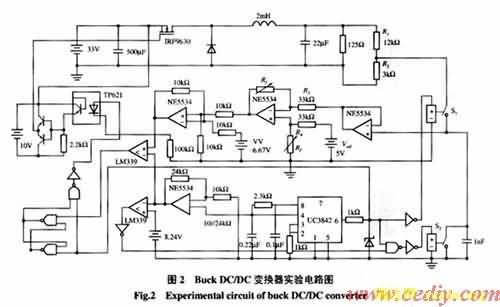
    达式根据图形可知为

式中  V_H、V_L是比较信号三角波峰值和谷值电压。
    图3是实验电路输出电压随反馈参数K变化，由稳定到分岔直至混沌的实验情况，由图中可见，其分岔点在0.1335处，与式(14)计算得到的分岔点完全相同，也与图4(b)采用式(11)精确离散模型仿真得到的分岔点相同，并且形状相同，从而实验和理论证明本文的精确离散模型的正确性，为便于比较，以上实验及仿真参数均与文[5]相同。图4(a)是以往采用纯数值仿真和近似离散模型分析得到的最好结果^[5]，从图中可见，其分岔点在0.12处，明显与实际分岔点不同，且形状也有较大差异。

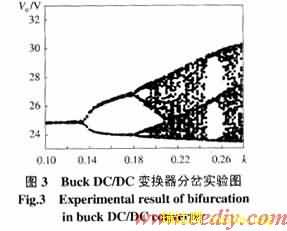
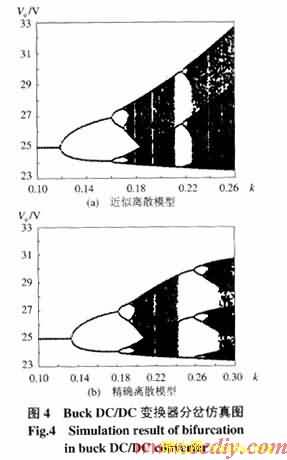
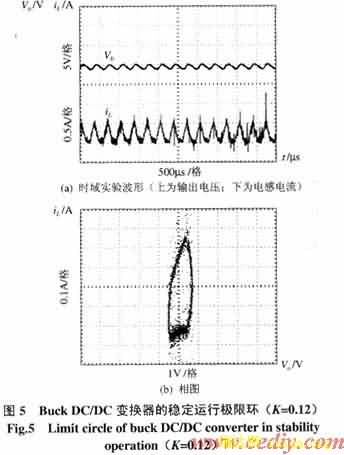
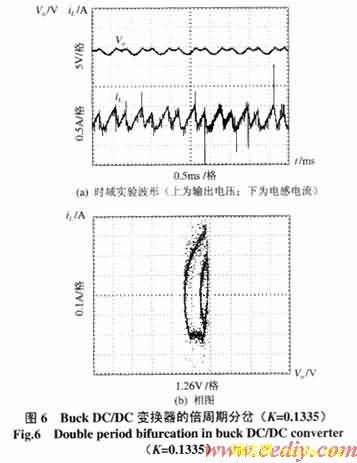
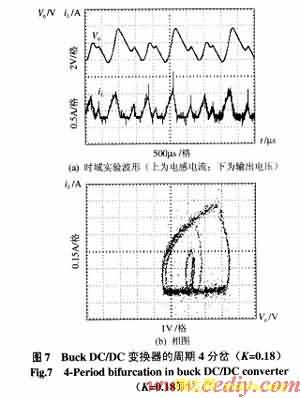
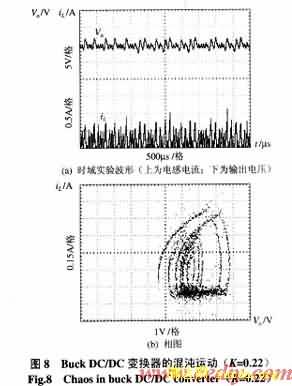
    图5~图8则分别是相应于不同反馈参数K下变换器电感电流和输出电压的时域实验波形及相图。从图中可以明显看出变换器从稳定工作，相图为一个极限环(图5)，到倍周期分岔(图6)，相图为2个极限环，进一步到4周期分岔(图7)，相图为4个极限环，然后，进入混沌状态，其时域波形失去了周期运动的特点，成为一种类似随机的状态，从相图中可以看到，此时的相图是由无数的极限环簇组成的。实际完整地展现出Buck DC/DC变换器从稳定、不稳定直至混沌演化的全过程。

5  结论
    仿真和实验证明所建立的BUCK DC/DC变换器的精确离散数学模型的正确性，精确界定了BUCK DC/DC变换器稳定工作范围，能真实反映变换器各变量间的解析关系，从而为BUCK DC/DC变换器的优化设计和控制提供了理论依据。实验电路和实验展现BUCK DC/DC变换器分岔和混沌的演化过程。
    此外，本文提出的分岔和混沌分析精确离散建模方法，是在一般性基础上提出来的，因而不仅适合于BUCK DC/DC变换器的非线性建模和分析，也适合于一般DC/DC变换器如BOOST、CUK等的非线性建模和分析，具有一般性。

参考文献

[1]  Deane J H B，Hamill D C．Instability，subharmonics，and chaos in power electronic systems[J]．IEEE Trans. Power Electron.，Jul. 1990，5(3)：260-268．
[2]  Hamill D C，Deane J H B，Jefferies D J．Modeling of chaotic DC-DC converters by iterated nonlinear mappings[J]．IEEE Tran. Power Electron.，Jan. 1992，7(1)：25-36．
[3]  Bernardo M di，Vasca F．Discrete-time maps for the analysis of bifurcations and chaos in DC/DC converters[J]．IEEE Trans. Circuits and Syst. I，Feb. 2000，47(2)：130-142．
[4]  Cheng K W E，Liu M，Wu J，et al．Study of bifurcation and chaos in the current-mode controlled buck-boost DC-DC converter[C]．in Proc. IEEE Industrial Electronics Society (IECON’01)，2001，2：838-843．
[5]  张波，齐群（Zhang Bo，Qi Qun）．PWM Buck 变换器不同工作方式下的次谐波和混沌行为（Subharmonics and chaos of PWM buck converter indifferent operation modes）[J]．中国电机工程学报（Proceedings of the CSEE），2002，22(10)：18-21．
[6]  张波，李萍，齐群（Zhang Bo，Li Ping，Qi Qun）．DC-DC变换器分*和混沌现象的建模和分析方法（Methods for analyzing and modeling bifurcations and chaos in DC-DC converter）[J]．中国电机工程学报（Proceedings of the CSEE），2002，22(11)：81-86．
[7]  Tse C K．Flip bifurcation and chaos in three-state boost switching regulators[J]．IEEE Trans. Circuits and Syst. I，Jan. 1994，41(1)：16-23．
[8]  Alfayyoumi M，Nayfeh A H，Borojevic D．Modeling and analysis of switching-mode DC-DC regulators[J]．International Journal of Bifur-cation and Chaos，2000，10(2)：373-390．
[9]  Bernardo di M．Garofalo F，Glielmo L，et al．Switchings, bifurcations, and chaos in DC/DC converters[J]．IEEE Trans. Circuits and Syst. I， Aug. 1998，45(2)：133-141．

瑞达币购买

桂山秋竹_唐年桂2023年

桂北云雾图_唐年桂202