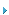摘要:介绍了重复控制器的基本原理,详述了重复控制器中一个关键参数对系统稳态误差和收敛速度的影响,总结设计该参数的两个方法。通过仿真分析,解释该参数的不同选择方案引起系统稳态精度不同的原因,提出了一些该参数的改进方法。
1引言
在逆变器中,采用SPWM技术,虽然控制方法简单,且易实现,但是同时也带来了很大的谐波成分。为了使逆变器输出在任何负载下都能够保证很高的精度,降低THD,提高系统的动态响应,一些复杂的控制思想已在逆变器的控制系统中得以应用,如滑模变结构控制[1]、极点配置[2]、模糊控制[3]等。重复控制策略最初是用于机械运动领域,但近年来其在逆变器中应用的优势越来越受到关注。这是由于在逆变器中,因非线性负载等众多因素引起的干扰一般都为高频且具有周期性,最终这种性质的干扰将导致输出波形的失真并具有重复性,所以利用重复控制器的特殊性质,能够大大消除输出波形的谐波。本文通过仿真研究,也进一步证明了利用重复控制技术来抑制谐波,降低THD,效果极佳。但是关于重复控制器中补偿器的设计,通常采用试凑法,尚未总结出一个普遍规律。本文试图通过进一步探讨补偿器的选择对误差的收敛精度和收敛速度的影响,总结其设计方案,并通过Matlab仿真证明,给出结论。
在逆变器中,采用SPWM技术,虽然控制方法简单,且易实现,但是同时也带来了很大的谐波成分。为了使逆变器输出在任何负载下都能够保证很高的精度,降低THD,提高系统的动态响应,一些复杂的控制思想已在逆变器的控制系统中得以应用,如滑模变结构控制[1]、极点配置[2]、模糊控制[3]等。重复控制策略最初是用于机械运动领域,但近年来其在逆变器中应用的优势越来越受到关注。这是由于在逆变器中,因非线性负载等众多因素引起的干扰一般都为高频且具有周期性,最终这种性质的干扰将导致输出波形的失真并具有重复性,所以利用重复控制器的特殊性质,能够大大消除输出波形的谐波。本文通过仿真研究,也进一步证明了利用重复控制技术来抑制谐波,降低THD,效果极佳。但是关于重复控制器中补偿器的设计,通常采用试凑法,尚未总结出一个普遍规律。本文试图通过进一步探讨补偿器的选择对误差的收敛精度和收敛速度的影响,总结其设计方案,并通过Matlab仿真证明,给出结论。
2重复控制器原理及参数选取分析
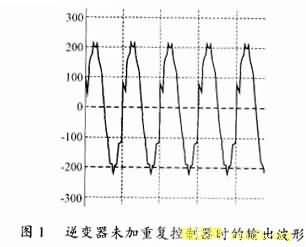
重复控制器能够特别有效地矫正周期性畸变的输出波形,保证输出波形精确跟踪给定。仿真中,给定为220V,50Hz的参考波,逆变器未加重复控制器前,输出波形参见图1(由于周期性扰动),加了重复控制器后,稳态时的输出波形参见图2。经对比,重复控制的优点显而易见。
重复控制器的基本框图参见图3,它是基于控制理论中的内模原理[2],即如果希望控制系统对某一参考指令实现无静差跟踪,那么产生该参考指令的模型必须包含在稳定的闭环控制系统内部。它把当前时刻t0输出与给定的误差e0不仅传到A(见图3),而且记忆下来,过了一个周期T后,把t0+T误差e1与e0相迭加后,传递到控制对象中进行控制,如此反复,即便输出与给定的误差e=0,A处仍有信号。
重复控制器能够特别有效地矫正周期性畸变的输出波形,保证输出波形精确跟踪给定。仿真中,给定为220V,50Hz的参考波,逆变器未加重复控制器前,输出波形参见图1(由于周期性扰动),加了重复控制器后,稳态时的输出波形参见图2。经对比,重复控制的优点显而易见。
重复控制器的基本框图参见图3,它是基于控制理论中的内模原理[2],即如果希望控制系统对某一参考指令实现无静差跟踪,那么产生该参考指令的模型必须包含在稳定的闭环控制系统内部。它把当前时刻t0输出与给定的误差e0不仅传到A(见图3),而且记忆下来,过了一个周期T后,把t0+T误差e1与e0相迭加后,传递到控制对象中进行控制,如此反复,即便输出与给定的误差e=0,A处仍有信号。
 '
'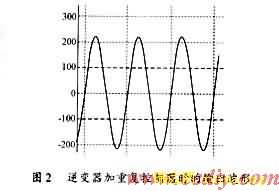
图3中虚线框中为重复控制器的内模,它实现了误差的记忆功能;N为一个周期内采样的次数,P(z)为逆变器的输出与输入的离散传函,可以通过测绘输出响应曲线获得[5],或者建立系统状态方程获得[6];S(z)须自行设计,用来修饰P(z)的参数,它的作用就是在中低频内与P(z)对消,而在高频内使P(z)增益急剧衰减[6];Q存在于重复控制器的内模之中,它是影响系统稳态精度与误差收敛速度的关键参数,是本文主要讨论的对象;zk是用来弥补系统相位差的一个量。
若不考虑扰动d,把图3进行变形,如图4所示。
若不考虑扰动d,把图3进行变形,如图4所示。
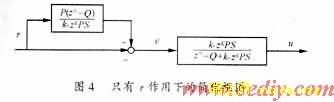
得
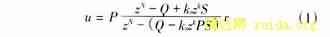
若不考虑给定r,把图3进行变形,如图5所示。
若不考虑给定r,把图3进行变形,如图5所示。
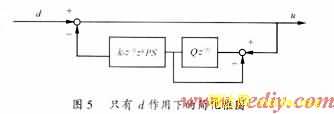
得

欲使系统稳定,特征方程
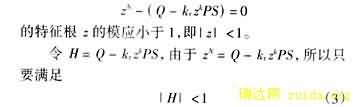
则系统稳定,且H越小,系统稳定裕度越大,收敛速度越快。若|H|=0,则就可以在一拍之内,使系统达到稳定。
欲使系统稳定,特征方程
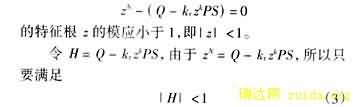
由式(1)可得:Q=1,当zN=1(稳态时),则u=r,即无静差。但若Q=1,则欲使|H|尽量小就相当苛刻,这是因为P参数难以精确获得,找到与P完全对消的函数就很难。究竟该如何取Q值,由式(2)可以发现:当zN=1(稳态时),

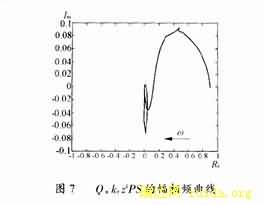
经上述分析,Q应为接近于1的数,而且与krzkPS的变化关系密切。为了满足稳定判据式(3),若以Q的轨迹为中心画一单位圆,那么仅当krzkPS在该单位圆内,系统才稳定(参见图6)[4][5]。经设计,最终做到了S与P在中低频对消,而放弃了它们在高频的对消,描绘出krzkPS的幅相频曲线如图7所示。krzkPS在低频段接近于1,而在高频段逐渐向平面左侧移动,且幅值迅速减小。
可以发现重复控制器中,Q是一个关键的设计参数。取Q的方法有两种[2][4][5]:
1)取Q为一个小于且接近于1的常数,这是为了保证krzkPS在高频时仍在以Q为圆心的单位圆内。
2)取Q为一个低通滤波器,则在krzkPS往左半平面移的时候,Q跟着往左移。
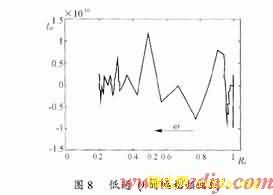
可以对照图7,图8(低通Q的幅相频曲线)看出来。
3.1Q取常数
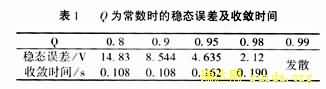
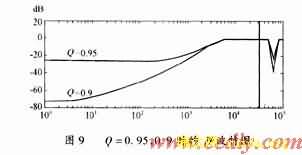
在仿真中,已设计好的模型取Q为一组常数,其稳态误差与收敛时间列于表1。研究对比Q=0.95,0.9的稳态误差及收敛时间可知:由于Q=0.9的H值小于Q=0.95的H值(见图9),所以Q=0.9的收敛速度略大于Q=0.95的收敛速度。但是稳态误差的大小却决定于 ,观察
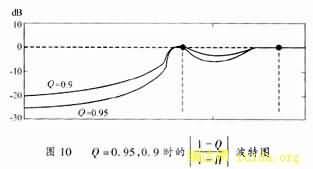
,观察 的波特图(见图10),Q=0.95
的波特图(见图10),Q=0.95 的值明显小于Q=0.9时的值,这就导致前者的误差小于后者的误差。因此,在设计中,收敛速度与收敛精度是需要互相权衡的两个量。在本系统仿真中,所取的众多常值中,Q=0.98的稳态误差最小。
的值明显小于Q=0.9时的值,这就导致前者的误差小于后者的误差。因此,在设计中,收敛速度与收敛精度是需要互相权衡的两个量。在本系统仿真中,所取的众多常值中,Q=0.98的稳态误差最小。
在仿真中,已设计好的模型取Q为一组常数,其稳态误差与收敛时间列于表1。研究对比Q=0.95,0.9的稳态误差及收敛时间可知:由于Q=0.9的H值小于Q=0.95的H值(见图9),所以Q=0.9的收敛速度略大于Q=0.95的收敛速度。但是稳态误差的大小却决定于
3.2Q取低通滤波器
当Q取作低通滤波器时,若设Q的分子为num(Q),分母为den(Q),

所以Q为一实数,其相位在0与π之间跳变,但在设计中,应把Q设为恒正量,这样就无须对它进行额外的相位补偿;且在中低频时,Q的增益略大于1,同时它的幅频曲线周期性地出现一个波谷,这个波谷所对应的频率的位置,可人为地通过改变各项系数加以调整,设计中把第一个波谷设在高频处,并与krzkPS迅速衰减处的高频相对应。
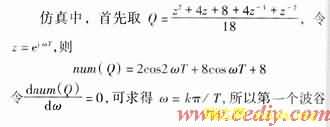
的位置在ω=π/T处。
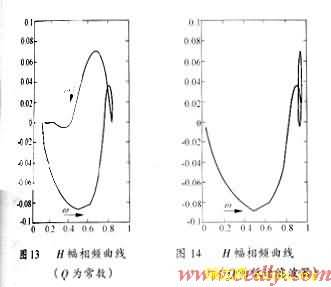
通过仿真实验发现依照这种方法选取的Q,其输出稳态误差比Q取作常数时更小得多(参见图11),这是因为低通Q实现了更好的跟踪krzkPS轨迹的效果,尤其是在高频的时候。比较图13,图14中H的幅相频曲线上可以很清楚 地反映不同Q跟踪krzkPS的过程。
当Q取作低通滤波器时,若设Q的分子为num(Q),分母为den(Q),

所以Q为一实数,其相位在0与π之间跳变,但在设计中,应把Q设为恒正量,这样就无须对它进行额外的相位补偿;且在中低频时,Q的增益略大于1,同时它的幅频曲线周期性地出现一个波谷,这个波谷所对应的频率的位置,可人为地通过改变各项系数加以调整,设计中把第一个波谷设在高频处,并与krzkPS迅速衰减处的高频相对应。
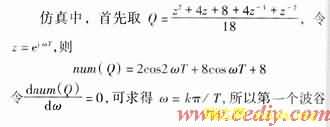
的位置在ω=π/T处。
通过仿真实验发现依照这种方法选取的Q,其输出稳态误差比Q取作常数时更小得多(参见图11),这是因为低通Q实现了更好的跟踪krzkPS轨迹的效果,尤其是在高频的时候。比较图13,图14中H的幅相频曲线上可以很清楚 地反映不同Q跟踪krzkPS的过程。


4结语
根据前面的讨论,在重复控制器的设计中,关于关键参数补偿器Q的设计,可以做出以下总结:
1)通过调节Q,可以提高系统的稳态精度,改善系统性能。
2)Q有两种选择:常数与低通滤波器,后者比前者的控制性能更优,但增加了软件实现上的难度。
3)当Q选取为低通滤波器时,若适当调节Q的分母,可以大大降低系统的稳态误差。