欧姆定律

简述：在同一电路中，导体中的电流跟导体两端的电压成正比，跟导体的电阻成反比,这就是欧姆定律。基本公式是I=U:R
　　(由欧姆定律I=U/R的推导式R=U/I不能说导体的电阻与其两端的电压成正比，与通过其的电流成反比，因为导体的电阻是它本身的一种性质，取决于导体的长度、横截面积、材料和温度，即使它两端没有电压，没有电流通过，它的阻值也是一个定值，永远不变。)

乔治·西蒙·欧姆
　　欧姆（1787年—1854年）是一个刻苦很勤奋的研究者。
　　欧姆第一阶段的实验是探讨电流产生的电磁力的衰减与导线长度的关系，其结果于1825年5月在他的第一篇科学论文中发表。在这个实验中，他碰到了测量电流强度的困难。在德国科学家施威格发明的检流计启发下，他把斯特关于电流磁效应的发现和库化扭秤方法巧妙地结合起来，设计了一个电流扭力秤，用它测量电流强度。欧姆从初步的实验中发出，电流的电磁力与导体的长度有关。其关系式与今天的欧姆定律表示式之间看不出有什么直接联系。欧姆在当时也没有把电势差（或电动势）、电流强度和电阻三个量联系起来。
　　在欧姆之前，虽然还没有电阻的概念，但是已经有人对金属的电导率（传导率）进行研究。欧姆很努力，1825年7月，欧姆也用上述初步实验中所用的装置，研究了金属的相对电导率。他把各种金属制成直径相同的导线进行测量，确定了金、银、锌、黄铜、铁等金属的相对电导率。虽然这个实验较为粗糙，而且有不少错误，但欧姆想到，在整条导线中电流不变的事实表明电流强度可以作为电路的一个重要基本量，他决定在下一次实验中把它当作一个主要观测量来研究。
　　在以前的实验中，欧姆使用的电池组是伏打电堆，这种电堆的电动势不稳定，使他大为头痛。后来经人建议，改用铋铜温差电偶作电源，从而保证了电源电动势的稳定。
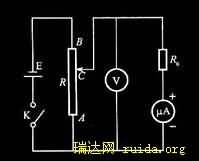
　　1826年，欧姆用上面图中的实验装置导出了他的定律。在木质座架上装有电流扭力秤，DD'是扭力秤的玻璃罩，CC'是刻度盘，s是观察用的放大镜，m和m'为水银杯，abb'a'为铋框架，铋、铜框架的一条腿相互接触，这样就组成了温差电偶。Ａ、Ｂ是两个用来产生温差的锡容器。实验时把待研究的导体插在m和m'两个盛水银的杯子中，m和m'成了温差电池的两个极。
　　欧姆准备了截面相同但长度不同的导体，依次将各个导体接入电路进行实验，观测扭力拖拉磁针偏转角的大小，然后改变条件反复操作，根据实验数据归纳成下关系：
　　x=q/(b+l)式中x表示流过导线的电流的大小，它与电流强度成正比，Ａ和Ｂ为电路的两个参数，Ｌ表示实验导线的长度。
　　1826年4月欧姆发表论文，把欧姆定律改写为：x=ksa/ls为导线的横截面积，K表示电导率，A为导线两端的电势差，L为导线的长度，X表示通过L的电流强度。如果用电阻l'=l/ks代入上式，就得到X=a/I'这就是欧姆定律的定量表达式，即电路中的电流强度和电势差成正比而与电阻成反比。为了纪念欧姆对电磁学的贡献，物理学界将电阻的单位命名为欧姆，以符号Ω表示。
　　电阻的单位欧姆简称欧。１欧定义为：当导体两端电势差为１伏特，通过的电流是1安培时，它的电阻为1欧。
　　一个导体的电阻R不仅取决于导体的性质，它还与工作点的温度有关。对于有些金属、合金和化合物，当温度降到某一临界温度T°C时，电阻率会突然减小到无法测量，这就是超导电现象。
　　导体的电阻与温度有关。一般来说，金属导体的电阻会随温度升高而增大，如电灯泡中钨丝的电阻。半导体的电阻与温度的关系很大，温度稍有增加电阻值即会减小很多。通过实验可以找出电阻与温度变化之间的关系，利用电阻的这一特性，可以制造电阻温度计（通常称为“热敏电阻温度计”）。

部分电路欧姆定律
　　部分电路欧姆定律公式：I=U/R
　　其中：I、U、R——三个量是属于同一部分电路中同一时刻的电流强度、电压和电阻。
　　Ｉ＝Ｑ／t　电流＝电荷量／时间 (单位均为国际单位制）
　　也就是说：电流＝电压/ 电阻
　　或者 电压＝电阻×电流『只能用于计算电压、电阻，并不代表电阻和电压或电流有变化关系』
　　欧姆定律通常只适用于线性电阻，如金属、电解液（酸、碱、盐的水溶液）。
　　由欧姆定律所推公式:
　　串联电路：
　　I总=I1=I2(串联电路中，各处电流相等)
　　U总=U1+U2（串联电路中，总电压等于各处电压的总和）
　　R总＝R1+R2+......+Rn
　　U1：U2=R1：R2
　　并联电路：
　　I总=I1+I2（并联电路中，干路电流等于各支路电流的和）
　　U总=U1=U2 （并联电路中，电源电压与各支路两端电压相等）
　　1/R总=1/R1+1/R2
　　I1：I2=R2：R1
　　R总=R1·R2\（R1+R2）
　　R总=R1·R2·R3：R1·R2+R2·R3+R1·R3
　　即1/R总=1/R1+1/R2+……+1/Rn

全电路欧姆定律(闭合电路欧姆定律)
　　I=E/(R+r)
　　V-电压-伏特
　　R-电阻-欧姆
　　I-电流-安培
　　其中E为电动势,r为电源内阻,内电压U内=Ir,E=U内+U外
　　适用范围:纯电阻电路
　　闭合电路中的能量转化:
　　E=U+Ir
　　EI=UI+I^2R
　　P释放=EI
　　P输出=UI
　　纯电阻电路中
　　P输出=I^2R
　　=E^2R/(R+r)^2
　　=E^2/(R^2+2r+r^2/R)
　　当 r=R时 P输出最大,P输出=E^2/4r (均值不等式)
　　功率与电阻的关系
　　欧姆定律例题
　　1.由欧姆定律导出的电阻计算式R=U/I，以下结论中，正确的为A、加在导体两端的电压越大，
　　则导体的电阻越大B、 通过导体的电流越大，则导体的电阻越小C、 导体的电阻跟它两端的电压成正比，跟电流成反比D、导体的电阻值等于导体两端的电压与通过导体的电流的比值。
　　2、一个导体两端加有电压为6V时，通过它的电流大小为0.2A，那么该导体的电阻为 Ω,若两端的电压为9V时,通过导体的电流为 A。若电路断开，那么通过导体的电流为 A。此导体的电阻为 Ω。
　　3、 一个导体两端的电压为15V时，通过导体的电流为3A，若导体两端的电压增加3V，那么此时通过导体的电流和它的电阻分别为
　　A 0.6A 5Ω B 3.6A 5Ω
　　C 3.6A 1Ω D 4A 6Ω
　　4、一只电阻当其两端电压从2V增加到2.8V时，通过该电阻的电流增加了0.1A，那么该电阻的阻值为
　　A 8Ω B 20Ω
　　C 28Ω D 18Ω
　　5、一个定值电阻阻值为20Ω，接在电压为2V的电源两端。那么通过该电阻的电流是 A。若通过该电阻的电流大小为0、15A，则需要在电阻两端加上 V的电压。
　　6、有甲、乙两个导体，甲导体的电阻是10Ω，两端电压为3V；乙导体电阻是5Ω，两端电压为6V。那么通过两导体的电流
　　A I甲=6V/10Ω=0.6A I乙=3V/10Ω=0.3A
　　B I甲=3V/10Ω=0.6A I乙=6V/5Ω=0.3A
　　C I甲=6V/5Ω=1.2A I乙=6V/10Ω=0.6A
　　D I甲=3V/10Ω=0.3A I乙=3V/5Ω=0.6A

欧姆定律的微分形式
　　在通电导线中取一圆柱形小体积元，其长度ΔL，截面积为ΔS，柱体轴线沿着电流密度J的方向，则流过ΔS的电流ΔI为：
　　ΔI＝JΔS
　　由欧姆定律：ΔI=JΔS=-ΔU/R 由电阻R＝ρΔL/ΔS，得：
　　JΔS＝-ΔUΔS/(ρΔL）
　　又由电场强度和电势的关系，-ΔU/ΔL=E，则：
　　J＝1/ρ*E＝σE
　　（E为电场强度，σ为电导率）
　　有关欧姆定律的公式（包括推出来的）

有关欧姆定律的公式（包括推导出来的）
　　由欧姆定律所推公式:
　　并联电路： 串联电路
　　I总=I1+I2 I总=I1=I2
　　U总=U1=U2 U总=U1+U2
　　1：R总=1：R1+1：R2 R总=R1+R2R
　　I1：I2=R2：R1 U1：U2=R1：R2
　　R总=R1+R2：R1R2
　　R总=R1R2R3：R1R2+R2R3+R1R3
　　也就是说：电流＝电压÷电阻
　　或者 电压＝电阻×电流
　　流过电路里电阻的电流，与加在电阻两端的电压成正比，与电阻的阻值成反比。
　　⑴串联电路 P（电功率）U（电压）I（电流）W（电功）R（电阻）T（时间）
　　电流处处相等 I1=I2=I
　　总电压等于各用电器两端电压之和 U=U1+U2
　　总电阻等于各电阻之和 R=R1+R2
　　U1：U2=R1：R2
　　总电功等于各电功之和 W=W1+W2
　　W1：W2=R1：R2=U1：U2
　　P1：P2=R1：R2=U1：U2
　　总功率等于各功率之和 P=P1+P2
　　⑵并联电路
　　总电流等于各处电流之和 I=I1+I2
　　各处电压相等 U1=U1=U
　　总电阻等于各电阻之积除以各电阻之和 R=R1R2÷（R1+R2）
　　总电功等于各电功之和 W=W1+W2
　　I1：I2=R2：R1
　　W1：W2=I1：I2=R2：R1
　　P1：P2=R2：R1=I1：I2
　　总功率等于各功率之和 P=P1+P2
　　⑶同一用电器的电功率
　　①额定功率比实际功率等于额定电压比实际电压的平方 Pe/Ps=(Ue/Us)的平方
　　2．有关电路的公式
　　⑴电阻 R
　　①电阻等于材料密度乘以（长度除以横截面积） R=密度×（L÷S）
　　②电阻等于电压除以电流 R=U÷I
　　③电阻等于电压平方除以电功率 R=UU÷P
　　⑵电功 W
　　电功等于电流乘电压乘时间 W=UIT（普式公式）
　　电功等于电功率乘以时间 W=PT
　　电功等于电荷乘电压 W=QU
　　电功等于电流平方乘电阻乘时间 W=I×IRT（纯电阻电路）
　　电功等于电压平方除以电阻再乘以时间 W=U•U÷R×T（同上）
　　⑶电功率 P
　　①电功率等于电压乘以电流 P=UI
　　②电功率等于电流平方乘以电阻 P=IIR（纯电阻电路）
　　③电功率等于电压平方除以电阻 P=UU÷R(同上)
　　④电功率等于电功除以时间 P＝W：T
　　⑷电热 Q
　　电热等于电流平方成电阻乘时间 Q=IIRt（普式公式）
　　电热等于电流乘以电压乘时间 Q=UIT=W（纯电阻电路）