New Fractional-N Synthesizer and Performance of Phase Noise 

    Abstract :Fractional-N technology resolve the contradiction between frepuency resolution and switching time in PLL synthesizer ，but result in severe phase noise ．Traditional method of phase compensation needs high performance of digital component such as A／D，and has time delay，so it is difficulty to achieve it ．ΔΣmodulator has plastic function to noise，resultlyN orderΔΣmodulatorused in Fractional N synthesizer can resolve the problem ofphase noise，and accelerate the development and using ofFractional N synthesizer．In the end the paper introduce the applid circuit of this new Fractional N synthesizerwhich wasrealized in GHZ frequency there ，and bring out the test performance of phase noise．
　　Keywords ：Fractional-N；phase noise ；ΔΣ modulation；A／D

    频率合成技术是将一个高稳定度和高准确度的基准频率经过四则运算，产生同样稳定度和准确度的任意频率。由于锁相环路具有高稳定性、优越的跟踪性能及良好的抗干扰性，在频率合成中得到了广泛应用。但是锁相环频率合成器中长期存在着频率分辨率和转换时间的矛盾，即提高频率分辨率，就必须减小参考频率f_r其结果导致转换时间延长。小数分频频率合成器则是对原来的整数分频进行了改进，通过采用小数的分频比来解决了频率分辨率和转换时间的矛盾，但是却引入了严重的相位噪声。传统的相位补偿的方法由于对数字器件的要求很高，并且具有一定的延时，所以不能很好地解决小数分频中的相位噪声。如果ΔΣ调制技术用到小数分频合成器中即解决了严重的相位噪声，又解决了频率分辨率和转换时间的矛盾。采用ΔΣ调制技术的小数分频频率合成技术是一种新型的频率合成技术，具有重要的研究价值和应用前景。

1　小数分频中的相位噪声产生原理
　　小数分频合成器的分频比是一个带小数的值N．F，由于数字分频器本身无法实现小数分频，因此小数分频是利用整数分频采用平均等效来实现的。其实现的原理图如图1所示。

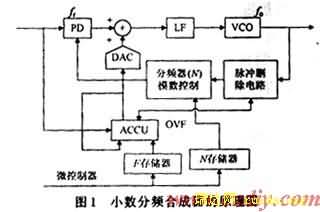
　　采用的方法是在每M个周期内并不全是N分频，而是其中a次为N分频，b次为N＋1分频(a＋b＝M)，这样平均每周期的分频比为：
 
 
　　显然MT_r在中分频器输出的平均频率等于f_r，但是瞬时频率不等，从而使鉴相器的输出存在一定的相位误差。当小数分频时，分频器输出脉冲周期为(N．F)T_o，当整数分频时，分频器输出脉冲周期NT_o，所以两者之间的差值为：
 
令 T_r＝1，ΔT为一个参考周期内参考信号比小数分频器输出的滞后时间值，化为相位差：
 
K个参考周期内，总相位误差为：

若K个参考周期内，从1到K周期内，无进位信号，则相位差以直线性增长：
 
若K个参考周期内，从1到K周期内，有L次进位(即L次N＋1分频)，则相位差减小L次：
 
    所以相位差信号为：
 

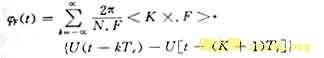
因此每经过一个T_r参考周期，相位差递增一个增量值，这个增量值为：
 
    由此可知，相位差是一个依次递增呈锯齿形的相差，举例说明，小数分频比为0．3即．F＝0．3，时其相位差波形如图2所示。

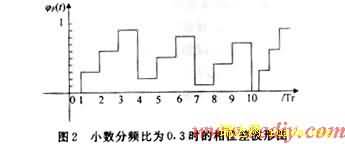
　　鉴相器的相位差输出通过环路滤波器时，其中较低频率的锯齿形噪声无法被滤除并直接输入到VCO，那么VCO的输出频率中将包含大量的相位噪声，大大降低了频谱的纯度。传统上可以采用相位补偿电路来消除相位噪声。如图1所示，将ACCU所存的数经过数模转换之后，恰好产生一个可以与小数杂散相抵消的锯齿波，但是此方法对数模转换器件要求很高，并且结构复杂，需要精心设计，且把相噪降到－70 dBC以下较难。采用ΔΣ调制技术的频率合成器无需任何补偿电路，性能分析表明他能得到具有很低杂波的信号输出。

2　ΔΣ调制器原理及其相噪整型分析
　　数字一阶ΔΣ调制器在Z域的数学模型如图3所示。

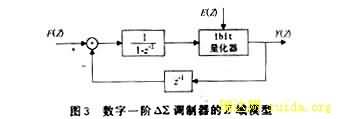
　　那么调制器的输出为：
 
　　由此可知数字一阶ΔΣ调制器无衰减传输信号，而高通滤除了他自己产生的量化噪声。小数分频合成器中的相位累加器和数字一阶ΔΣ调制器具有相同的数学模型，由于他的相位噪声主要在低频端，所以累加器对其自身的量化误差的滤波性能十分有限，因此应该采用多级级联的方式来对量化噪声进行整形。以下是三阶级连的ΔΣ调制器，其模型如图4所示。

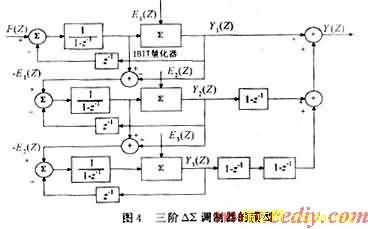
    由图4可推导出三阶ΔΣ调制器的分频比输出为：　

    由此可知采用多阶ΔΣ调制器利用其对噪声的整型功能，将量化噪声从低频端推向高频端。并且ΔΣ调制器阶数越大，在高频端的噪声功率也越，噪声整型效果越好。在频率合成器中鉴相器的输出信号在输入到VCO之前需要经过环路滤波器对噪声进行滤波，而滤波器的带宽大小也在很大程度上决定了通过低通滤波器的相位噪声大小。因此在小数分频合成器中采用多阶ΔΣ调制器，并且选用适当的环路滤波器，可以得到良好频谱的输出频率。下面介绍采用硬件电路实现的采用ΔΣ调制技术的频率合成器并测得良好的性能指标。

3　新型小数分频合成器的电路实现和测试性能
　　从ΔΣ调制器的理论分析中知道采用三阶以上的ΔΣ调制器来对噪声进行整型，在低频端的相位噪声可以达到很小。本文采用的是专用集成芯片cx72301来实现，其内部采用四阶ΔΣ调制器。在外加环路滤波器、压控振荡器、晶体振荡器、单片机控制器等器件构成，电路如图5所示。

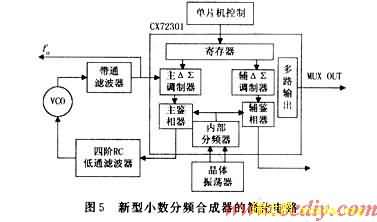
　　全数字化的集成芯片cx72301简化频率合成器的电路，并且可以通过单片机进行控制，方便简洁。本电路由外部晶体振荡器提供参考晶振，芯片内部由一个内部分频的模块可以选择实际的参考频率(如24 MHz晶体输入，内部采用2分频，则实际芯片采用的参考频率为12 MHz)，芯片内部的各控制信号和欲输出的频率都进行数字化，通过单片机输入到内部的寄存器中，当所有信息被设置好，芯片上电(＋3 V)工作，内部的ΔΣ调制器由寄存器的储存信息控制，然后输入到鉴相器，由于鉴相器是集成在芯片内部的，所以外部只看到鉴相器的输出端。
　　由于鉴相器输出端中含有大量的高频干扰信号，因而要通过滤波器来滤除。外部采用了模拟的四阶级联的RC滤波器，由于滤波器带宽将影响系统的转换时间，所以经过对系统性能的综合考虑，设计其3 dB带宽为100 kHz。经滤波后的信号近似直流信号输入到VCO， VCO的输出频率可达GHz量级(590～1 000 MHz)。由于器件无法达到理想的线性化，因而输出的频率会出现一定的谐波，需要通过带通滤波器加以滤除，这样从端可以输出高纯度的频谱。当设置输出频率为700．555 55 MHz时，采用Agilent公司的高精度频谱分析测试得到的频谱和相位噪声性能如图6所示。

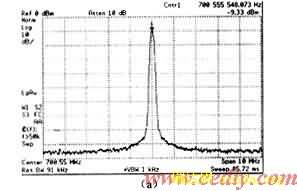
　　由测试的相位噪声波形图6(b)可以知道在偏移主频1 kHz时，相噪为－83 dB／Hz左右，当偏移主频10 kHz时，相噪为－93．78 dB／Hz。从而有力地说明了在小数分频合成器中采用ΔΣ调制技术可以很好地解决其内部量化产生的严重的相位噪声。

4　结　语
　　把具有噪声整型功能的ΔΣ调制器用于小数分频合成器构成新型的频率合成器，很好地解决了小数分频技术的相位噪声问题，并从理论上和实际电路测试的性能上证实了这一点，为小数分频技术的发展和应用提供有价值的参考。这种新型的小数频率合成器，具有优良的频谱性能，并且实现方便、简单，具有广阔的应用前景。