 打印本文
打印本文  关闭窗口
关闭窗口 关键词:PSK;频率估计;谱估计;修正协方差
1 引 言
在盲信号处理中,PSK信号的载频估计问题是实现PSK识别解调的首要问题,对中心载频做出准确估计非常重要。由于接收到的信号是一个随机过程,每次接收到的信号是该随机过程的一个样本,在噪声的影响下,每个样本的傅里叶变换都不尽相同。PSK是一种抑制载波的调制方法,在频域表现为有效带宽内的一片谱线,其傅里叶变换的最大值往往并不出现在中心载频位置。因此,直接利用傅里叶变换进行频率估计并不可靠,应该从统计学的角度来描述此随机信号的特征,本文应用现代谱估计方法进行估计。
经典谱估计方法以傅里叶变换为基础,无法解决频率分辨率低和谱估计稳定性之间的矛盾。因此针对其分辨率低和方差性能不好等问题提出了以随机过程的参数模型为基础的现代谱估计方法。现代谱估计方法具有更高的频率分辨率和更好的性能,大致可分为参数模型谱估计方法和非参数模型谱估计方法。MUSIC算法属于非参数型谱估计,而修正协方差法属于参数模型谱估计方法。
在对PSK信号参数估计方法中,修正协方差法看来是最好的频率估计器,他得出的频率估计对于正弦信号的相位最不敏感,而且由噪声影响而产生的谱蜂偏移也比其他AR方法小,没有噪声时,可以证明修正协方差法能够从谱峰估计出真实频率,但是对于其他AR估计器,这是不可能的[1]。
在比较各种谱估计方法时,应适当考虑到计算的复杂程度。总的说来,特征分析技术的计算量非常大,而修正协方差法计算量适中。
2 基本原理
2.1 Welch法
性质上属于周期图法,是经典谱估计方法中间接法的改进方法。

由于周期图的方差随记录数据长度的增加而不减小,因此为了改进周期图的统计特性,可以近似地用一组周期图进行平均的方法完成期望运算。Welch提出了平均周期图的改进方法,对每个数据段加窗并使数据段互相重叠。对于窄带分量,数据窗压低了谱估计的旁瓣电平从而减少泄漏,减少方差,这就是修正周期图法,也就是PSD估计的Welch方法。
2.2 多信号分类法(MUSIC)
MUSIC是用噪声子空间估计频率的一种算法,由于主特征向量(V1,V2,…,VM)组成的子空间和信号矢量(e1,e2,e3,…,eM)组成的子空间相同,而且特征矢量是相互正交的,所以信号矢量(e1,e2,e3,…,eM)与噪声子空间中的所有矢量也是正交的,即:
弦波的频率估计。其中f表示频率;e表示信号矢量。
2.3 本文提出的新方法
此方法基于修正协方差谱估计方法。
对于AR(p)过程,最佳前向预测:
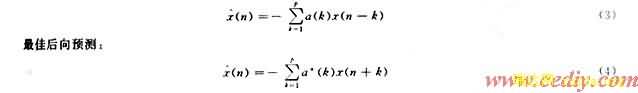
在这两种情况下,最小预测误差功率正好是白噪声方差σ2。
修正协方差法是以AR(p)过程前向预测误差功率和后向预测误差功率估计的平均值最小为准则估计AR模型参数。其准则为:
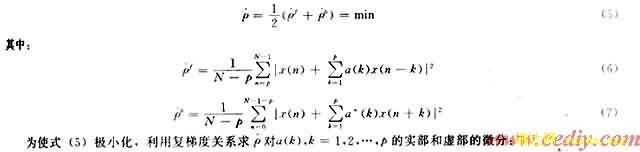
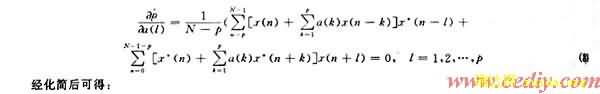
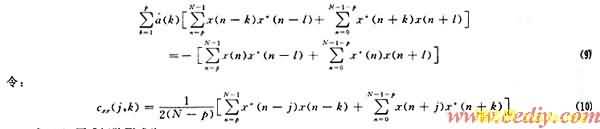
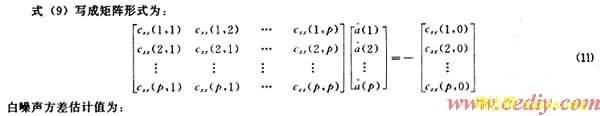
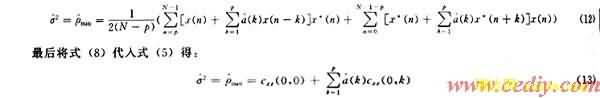
解方程组(12),(13)最终可得到频率估计。
实数据的协方差法是一种近似MLE方法。当RSN足够高时,修正协方差法用多项式求根来估计频率是无偏的,并且几乎达到CR界,可以得到高分辨率的统计稳定的谱估计值。对于由白噪声中的正弦信号组成的数据,该估计器的许多良好的特性已经可以从计算机的仿真结果中观察到。但是,当RSN较低时估计效果很差,出现偏差和较大的方差[2,3]。
为了充分利用修正协方差谱估计方法的这些良好特性,并改善其在较低信噪比下的估计性能,本文提出的新方法中对PSK信号做了预处理。由于理想PSK信号,其包络恒定,在通过匹配滤波器和受噪声影响后的窄带PSK信号的包络是渐变起伏的,所以在利用现代谱估计方法进行频率估计前先对PSK信号进行幅度整型,使其成为近似衡包络,以减小滤波和噪声对PSK信号瞬时幅度的影响而造成谱估计的误差的增加,仿真结果表明这对减小谱估计的误差具有一定改善。理想PSK信号的功率谱围绕信号中心载频近似对称,而当信噪比较低时,噪声会引起谱估计结果中谱峰的偏移。
所以估计结果并不以最大值作为频率估计的直接结果,而是在找到谱估计峰值时,以此为基础设定一个门限,得到超过这个门限且包含谱峰位置的一个区间,把区间的中心位置作为频率估计的最终结果。仿真结果表明此方法取得了较好的实际效果。
3 计算机仿真
本方法的计算机仿真实现由Matlab完成。首先产生PSK(BPSK,QPSK和8PSK)信号s(t),再加以窄带高斯白噪声n(t)。信号形式为:
为了验证此方法的有效性和稳定性,本文分别对其随信噪比变化,随数据长度变化以及随信号中心频率变化的估计性能做了仿真实验。
3.1 仿真一
仿真信号的信噪比由5 dB增加到25 dB,并对应每个信噪比独立运行20次,取相对误差的平均值作为估计误差,与Welch法和MUSIC算法得出的结果加以比较。其中带内噪声指的是以信号载波中心频率为中心一定带宽内的窄带噪声。
仿真中的信号参数如下:
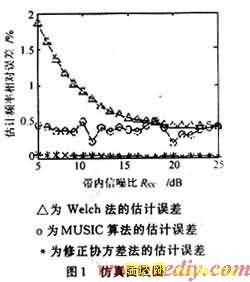
仿真实验以BPSK为例,信号中心载频为4 300 Hz,采样频率为44 100 Hz,调制信号码元速率为120 b/s,仿真产生的码元个数为60,窄带噪声带宽为600 Hz,仿真结果如图1所示。
由图1可以看出,在较低信噪比下Welch法精度较差,而MUSIC算法和修正协方差法仍具有很好的估计精度,而且随着信噪比的增加,估计误差不断减小,修正协方差法性能明显优于Welch法和MUSIC算法。
3.2 仿真二
检验新方法随着数据长度变化的估计性能的稳定性,并与Welch法和MUSIC算法得出的结果加以比较。
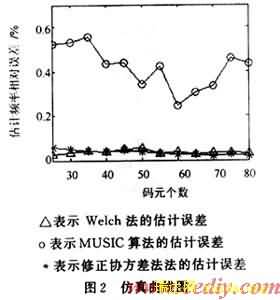
仿真实验以BPSK为例,采样频率降为22 000 Hz,信号中心载频为4300 Hz,调制信号码元速率为120 b/s,窄带噪声带宽为600 Hz,信噪比为10dB,仿真产生的码元个数从25个增加到80个。对应每个码元长度独立仿真20次,取相对误差的平均值作为估计误差。仿真结果如图2所示。
由图2可以看出,在码元个数较少时,修正协方差算法的估计性能优于Welch法,而比MUSIC算法稍差,当码元个数增加时,性能稍优于MUSIC算法。Welch法的估计性能明显不如另外两种方法。
4 结 语
计算机仿真实验结果表明,利用现代谱估计方法可以有效地估计PSK信号的中心频率,其中修正协方差法具有良好的抗噪声性能和较好的稳定性,且估计结果优于Welch法和MUSIC法。对于修正协方差功率谱估计方法,由于估计PSK信号的中心频率时,并不需要分辨相邻谱线,只需找到中心频率的位置。
因此在进行谱估计时并不需要很高的阶数,可以获得较快的运算速度,仿真实验中其效率远远高于Welch法和MUSIC算法。而且在数据长度较小或信噪比较低时都具有较好的估计效果,是一种高效的PSK信号的中心频率估计方法。
参考文献
[1][美]凯依SM.现代谱估计[M].北京:科学出版社,1994.
[2]Lang S W, McClellan J H .Frequency estimation with maximum entropy spectral estimators[J]. IEEE Trans.Acouss.,Speech Signal Process,1980,ASSP28(11):716-724.
[3]Tufts D W,Kumaresan R.Estimation of frequencies of multiple sinusoids making linear prediction perform like maximum likelihood[J].Proc,IEEE,1982,70(9):975.
 打印本文
打印本文  关闭窗口
关闭窗口