1 引言
    PWM变换器本质上属于强非线性系统，基于线性反馈控制的变换器在动态响应和鲁棒性上很难取得满意的控制效果。近年来，国内外学者将一些非线性控制方法引入PWM变换器中，如模糊控制^[1]，滑模控制^[2]，单周控制^[3]等。模糊控制和滑模控制能够改善PWM变换器的动态响应，但控制策略比较复杂。单周控制原理简单，易于工程实现，已被应用在一些基本变换器如Buck和Cuk变换器^[4]等，同时还推广至音频功率放大器^[5]、功率因数校正^[6]以及单相有源滤波器中^[7]，是目前较成功的非线性控制方法。但是单周控制开关变换器也存在不足，主要表现在三个方面：一是控制器对开关误差校正能力有限，系统存在稳态误差；二是当变换器因负载扰动从电感电流连续模式进入不连续模式时，系统会出现不稳定；三是变换器对负载扰动抑制能力差，负载动态响应慢。文献[5]介绍了一种改进的开关误差校正方案，通过引入两套积分回路进行周期切换，使开关误差降至最小。但两套积分回路元件参数必须严格匹配，否则输出纹波会明显增大，电路复杂。文献[6]将输出电压误差引入积分器，负载扰动抑制有所改善，但负载扰动信号是基于输出电压误差，受滤波器时间常数影响，因此不能实现最优动态响应。文献[7]通过检测每个开关周期的电感电压平均值，并引入到积分器来改善系统动态响应。该方案与文献[6]存在同样弊端。
    本文提出一种具有工程最优动态响应的PWM开关变换器非线性控制新策略，根据控制原理命名为“准周期积分函数控制”。系统改变了非线性积分器的复位方法，采用等间隔反向线性复位，强制开关变量平均值在每一个完整的开关周期中严格等于控制基准，彻底解决了因电力电子器件开关时间导致的开关误差，实现了开关变换器在输入电源变化时的零稳态误差。利用带自动积分限幅功能的控制器，在电感电流连续或不连续两种工作模式、以及临界状态下，系统均能可靠稳定的工作。采用带双前馈补偿的控制器，系统对负载扰动具有极好的抑制能力，实现了工程最优动态响应。新策略具有良好的通用性，适用于硬开关或软开关的Buck、Cuk、半桥或全桥变换器，以及由他们派生出来的其他变换器。仿真结果证明了新方案的合理性和有效性。
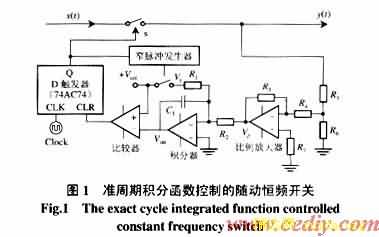
2  准周期积分函数控制基本原理
    准周期积分函数控制的恒频开关基本原理如图1，工作波形如图2所示。当恒定振荡频率的时钟脉冲（Clock）上升沿到来时，触发器置位，同时驱动开关S导通，开关输出y(t)等于输入信号x(t)，y(t)经采样电阻分压和放大器反向后变为V_p，并通过积分器积分，积分器输出V_int从初值V_r1开始向正方向线性增长。当V_int达到控制基准V_ref时，比较器输出翻转，触发器复位，开关S关断。关断信号同时控制窄脉冲发生器产生复位信号，使积分器复位开关w闭合，利用控制基准V_ref对积分器反向线性复位。该方案与单周控制的本质区别在于，每个开关周期中积分器输出没有复位至零，而是根据y(t)大小自动复位至某一个初值（如V_r1）。下一个时钟周期Clock到来时，积分器则从初值重新开始积分。

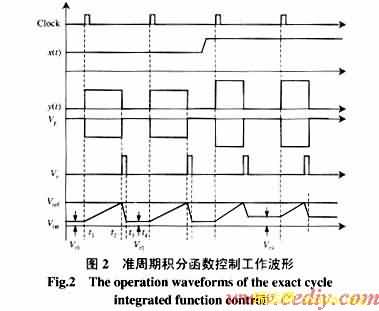
    积分器初值V_r2用下式计算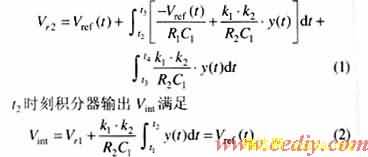

式中  k₁、k₂分别为采样电阻分压比及放大器增益；
    当系统进入稳态时，相邻开关周期的积分器初值相等，即V_r1= V_r2，因此

    式中左边的积分期间为整个开关周期T_s，而不是单周控制中的开关导通时间T_ON。因此在积分电容复位期间及其之后的时间段内（下一个时钟脉冲到来之前），被控开关的全部输出信息都进入积分器，保证复位期间不丢信息，实现开关误差的彻底校正和变换器零稳态误差。式(4)的物理意义是：被控开关变量y(t)在每一个完整的开关周期中的平均值严格等于控制基准V_ref(t)在复位期间的积分值。
3  开关误差产生机理及自动校正
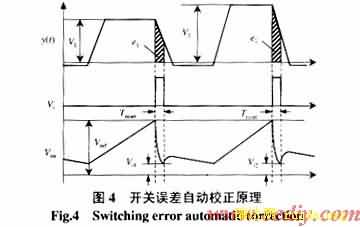
    非线性积分器和复位电路是单周控制^[3]的核心，为了保证控制精度，在每一个工作周期中积分器都必须复位至零。但由于复位电路时间常数不能做到无限小，复位不能瞬时完成，因此引起控制误差并导致系统的稳态误差（如图3）。

       复位过程中积分器输出用下式计算

式中  R和C分别为复位开关通态电阻和积分电容。
    理论上积分器需经无限长时间，放电才能结束，但实际上只要经过3t ~5t（t =RC为放电时间常数），就可近似认为放电基本结束。因此积分器最短复位时间T_reset必须大于3t ~5t。当输入信号发生变化时（如V₁<V₂），控制器的开关误差为

    △e大小与T_reset和输入信号变化幅度有关。开关误差将导致系统产生稳态误差，当T_reset远小于主开关的关断时间T_off时，开关误差才可忽略。
    本文提出的积分器复位新方法没有采用并联开关复位（图4），而采用窄脉冲线性反向复位。

    每个开关周期中积分器不完全复位到零，而是根据y(t)动态值，自动复位到某一个初值。y(t)越大，积分器初值也越大，则下一个周期中V_int达到V_ref的时间相应变短。相邻开关周期的积分器初值之差与开关误差成正比

式中  k为比例系数。
    如果相邻开关周期期间，输入信号未发生变化，则DV_i=0。该方案确保了每个开关周期中不丢失任何被控开关的输出信息，实现了开关误差彻底校正和变换器零稳态误差。
    新积分器复位方法与单周控制复位方法相比，对积分器复位时间T_reset（即窄脉冲宽度）的限制大大放宽，设计时只要满足下列条件，即可保证变换器正常工作

式中  t_r、t_f  分别为积分复位开关W的开关特性对应的上升和下降时间（可查器件手册）；D_max为变换器工作时的最大占空比；f_s为变换器工作频率。
    显然，式(8)为积分器复位时间T_reset提供了一个很宽的选择范围，准周期控制策略的积分器设计和器件选择比单周控制更容易工程实现。
4 准周期积分函数控制Buck变换器
    将准周期积分函数控制策略应用于Buck变换器，其原理如图5所示，被控开关变量反馈信号取自二极管电压V_D，恒频时钟Clock脉冲通过控制器（D触发器）触发开关管S导通，二极管电压V_D经采样电阻分压和放大器反向处理后，积分器开始对V_D积分，积分输出V_int从初值开始向正方向线性增长。

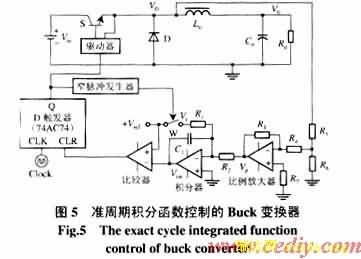
    当V_int达到控制基准V_ref时，比较器输出翻转，触发器复位将开关管S关断。同时关断信号触发窄脉冲发生器产生一个恒定脉宽的复位信号，使复位开关W闭合，对积分器反向线性复位。经过T_reset时间后，复位脉冲撤销，积分器被复位至初值V_r1。下一个时钟周期到来时，积分器则从该初值重新开始积分，周而复始。
5  电感电流不连续模式与积分饱和
    准周期积分函数控制或单周控制的开关变换器，当负载扰动使变换器从电感电流连续模式进入不连续模式时，会引起积分饱和导致系统不稳定。原因是电感电流不连续期间，二极管电压V_D等于输出电压V₀，而此时V₀由于负载扰动出现了超调，其峰值大于系统稳定时的输出稳态值（图6）。

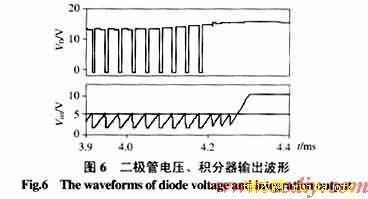
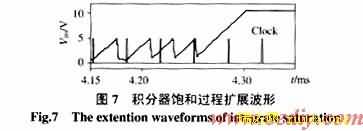
    因此，在积分器从初值开始积分到下一个clock到来前，就有可能出现积分器输出达到控制基准并使比较器状态翻转，由于此前控制器因负载扰动处于关断状态，因此触发器将不能正常产生复位信号，于是积分器将继续积分并最终导致饱和（图7）。而正常稳态情况下，始终处于电感电流不连续模式的变换器不会出现上述情况，因为此时的二极管电压V_D等于输出电压V₀，因此V_D在一个开关周期内的平均值不会超过控制基准，也就不会出现积分饱和。

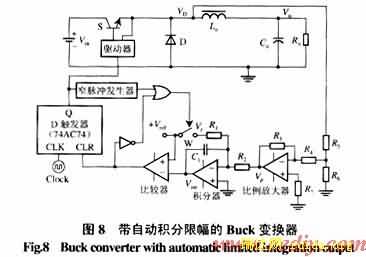
    本文提出一种具有自动积分限幅功能的准周期积分函数控制原理（如图8）。控制系统中增加了一个“或门”。当负载扰动导致电感电流不连续时，窄脉冲发生器不能产生复位信号，而比较器输出脉冲则承担了复位任务，且复位脉冲宽度不恒定，一旦积分器输出V_int小于控制基准V_ref，复位脉冲将自动撤销，因此积分器输出被箝位在V_ref附近，V_int的波动范围与复位时间常数、逻辑电路切换时间等有关。当变换器输出电压超调量变为负值，积分器自动脱离饱和状态，时钟脉冲可正常触发开关管导通，积分器恢复正常工作，系统进入稳态。上述附加电路相当于为积分器设置了一个自动积分限幅电路，且限幅值可随控制基准自动调节。

6 前馈控制及最优动态响应
    自动控制系统中，前馈控制比反馈控制更为及时。就PWM开关变换器而言，负载电流是一个外部扰动信号，因此引入负载电流前馈控制，只要电路设计合理，将可以显著改善变换器的负载动态响应，但由于输出滤波器时间常数的影响，前馈控制器不可能完全补偿负载电流扰动对输出电压的影响，即输出电压波动不可能完全消除，存在所谓的最优动态响应。
    图9为理想情况下变换器突加负载时引起的最小电容电压偏移波形图，图中不考虑滤波电容的等效串联电阻R_ES，忽略纹波电压和纹波电流，并假设前馈控制器为理想控制器。

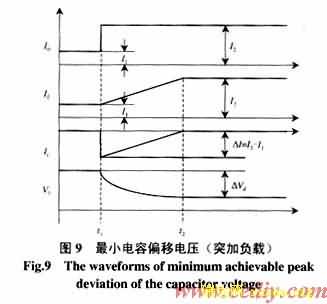
    假设t₁时刻，变换器突加负载，负载电流从I₁跃升至I₂，前馈控制器检测到负载扰动信号后，立刻触发开关管开通，由于滤波电感的存在，电感电流I_L将从稳态值I₁线性增长，t₂时刻上升至稳态值I₂。令过渡过程所用时间为Dt= t₂- t₁

    过渡期间负载电流不足部分由滤波电容放电提供。理想情况下，I_c放电斜率等于电感电流增长斜率，电容放电过程可表示为

7 带双前馈补偿的准周期积分函数控制Buck变换器
    在Buck变换器中，稳态电容电流是一个周期脉动信号，其纹波峰峰值为

式(13)表明，电容电流i_c的纹波幅值与输出电压成比例，因此i_c能很好地表征负载扰动。但是i_c还与输入电压V_in相耦合，V_in变化时i_c也变化，因此基于线性反馈控制或单周控制的PWM变换器不能直接检测i_c作为前馈信号，而只能检测负载电流。本文提出一种简单的双前馈控制方案（如图10）。

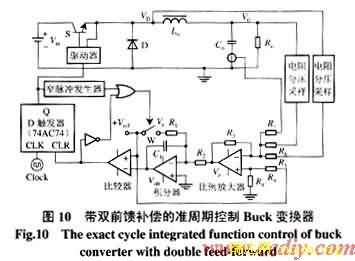
       电容电流i_c和输出电压误差V_e均作为前馈信号，并直接与二极管电压V_D进行求和，其输出作为积分器输入，系统中无需增加额外的前馈校正环节。引入双前馈扰动信号后，积分器输出为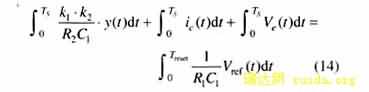

式中  左边第一项为V_D在一个周期内的平均值；第二项为i_c在一个周期内的平均值，由于i_c在稳态时是关于横轴对称的周期信号，因此其在一个周期内的平均值等于零，与V_in变化无关；第三项为V_e在一个周期内的平均值，稳态时V_e等于零，因此带双前馈补偿的积分器输出在稳态时与未引入前馈的控制器相同

以上分析表明，带双前馈补偿的控制器可实现对输入电压变化的静态无差。
8 仿真结果及分析
    应用电路仿真软件PSPICE对带双前馈补偿的准周期积分函数控制Buck变换器进行了仿真，电路参数如下：V_in=15V，f_s=30kHz，L₀=480mH，C=30mF，R₀=5W。仿真过程中考虑了实际的电路驱动能力和功率管开关时间。
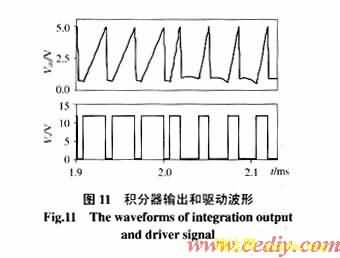
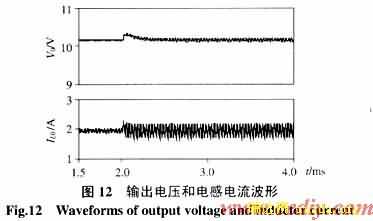
    （1）输入电源扰动抑制（图11、12）。系统控制基准和负载保持不变，变换器输入电源V_in由15V跃变到30V时，由仿真波形可以看出，V_int在每个开关周期中没有复位到零，从而实现了对开关误差的彻底校正。变换器对输入电源扰动具有极好的抑制能力，并实现了零稳态误差。

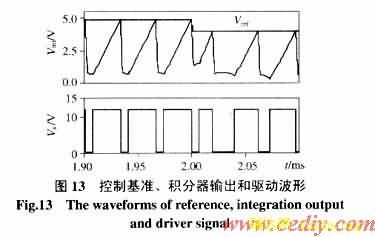
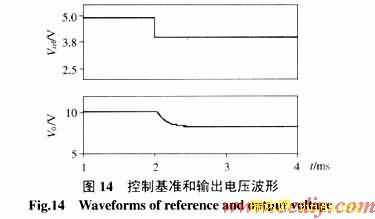
       （2）跟踪控制基准（图13、14）：系统输入电源和负载保持不变，控制基准V_ref产生阶跃变化，控制器将适时调整开关占空比，使变换器输出从前一个稳态值V₀₁快速过渡到新的稳态值V₀₂。仿真波形说明，变换器能很好地跟踪控制基准，系统具有良好的跟随性能。

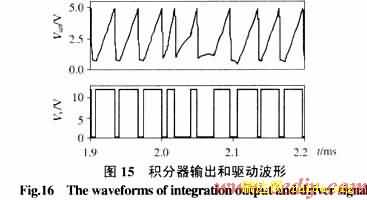
       （3）负载扰动抑制（图15、16）。变换器输入电源和控制基准保持不变，负载电流从2A突减到1A。由仿真波形看出，变换器输出电压的最大过冲为1V，暂态过渡过程为0.5ms。按照最优动态响应计算公式(16)，理想情况下输出电压的最小偏移量为0.82V。仿真结果说明，带双前馈补偿网络的控制器，其对负载扰动的抑制能力显著改善，抑制效果达到工程最优动态响应。
    （4）电感电流不连续模式（图17、18）。

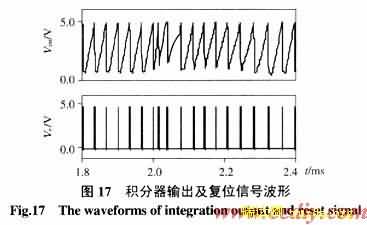
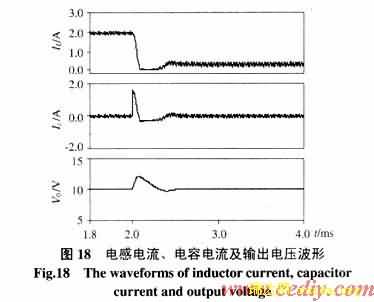
       当负载电流从2A突减到0.25A时，输出电压受到扰动并使电感电流进入不连续模式，此后，积分限幅电路开始工作，将积分器输出限制在控制基准以下。0.6ms以后，积分器退出饱和恢复正常工作状态，系统进入稳定状态。
9 结论
    （1）准周期积分函数控制通过引入非线性积分器，并采用等间隔反向线性复位法，强制被控开关变量平均值在每个完整的开关周期中严格等于控制基准，彻底解决了开关误差的自动校正问题，实现了变换器的零稳态误差。
    （2）利用带自动积分限幅功能的准周期积分函数控制器，变换器在电感电流连续或不连续模式、以及临界状态下，均能可靠稳定的工作，解决了临界状态下系统振荡问题。
    （3）利用带双前馈补偿的准周期积分函数控制器，变换器的负载扰动抑制能力显著改善，实现了工程最优动态响应。
    （4）准周期积分函数控制新策略具有良好的通用性，适用于各种硬开关或软开关的Buck、Cuk、半桥或全桥变换器，以及由他们派生出来的其他变换器。

参考文献

[1]  So W C，Tse C K，Lee Y S．A fuzzy controller for DC-DC converters[C]．IEEE PESC，Taipei，1994：315-320．
[2]  Venkataramanan R，Sabanovic A，Cuk S．Sliding mode control of DC-to-DC converter[C]．San Francisco，USA IECON’1985：251-258．
[3]  Smedly K M，Slobodan Cuk．One-cycle control of switching converters [J]．IEEE Trans. on Power Electronics，1995，10(6)：625-633．
[4]  Smedly K M，Slobodan Cuk．Dynamics of one-cycle controlled Cuk converters[J]．IEEE Trans. on Power Electronics，1995，10(6)： 634-639．
[5]  Zheren lai，Smedly K M．A new extension of one-cycle control and its application to switching power amplifiers[J]．IEEE Trans. on Power Electronics，1996，11(1)：99-105．
[6]  林维明（Lin Weiming）．PWM型DC/DC开关变换器非线性闭环控制策略的研究（Research on nonlinear control strategy for PWM DC/DC converters）[J]．中国电机工程学报（Proceedings of the CSEE），2001，21(3)：19-22．
[7]  林维明（Lin Weiming）．具有快速负载动态响应的DC/DC开关变换器开换控制新策略（A　new open-loop control strategy for a DC/DC switching converter with fast load transient response）[J]．中国电机工程学报（Proceedings of the CSEE），2001，21(9)：78-81．