1 引言
    随着功率半导体器件和微机控制技术的不断发展，开关电源越来越受到人们的重视。低开关应力、高功率密度、体积小、重量轻以及良好的动静态性能，都已成为人们追求的目标，因此，高频软开关技术在开关电源中获得了广泛应用。
    针对如何更有效地将直流电源转换为单相供电电源，很多文献进行了研究。其中，文献[1]提出半桥LCC谐振电路，利用正弦半波参考信号与实际输出电流进行滞环比较，来控制开关动作，这样使得开关频率变化取决于电流滞环范围，不利于滤波电抗器设计。文献[2]提出了双串联谐振的移相控制电路，由于该电路具有两套相同的半桥谐振电路，所以结构显得比较复杂，而且两套谐振电路的电感电流和电容电压不对称，以及当谐振参数不对称时，存在影响电气性能的缺点。文献[3]提出单极性移相控制高频脉冲交流环节逆变电路，变压器原边绕组电压为双极性三态高频脉冲交流电压波，为周波变流器开关提供了ZVS开关，但变压器原边电路为硬开关。文献[4]提出移相控制和有源整流相结合电路，实现了部分软开关。
    本文结合上述电路优点，提出利用恒频移相SPWM控制的LCC谐振电路，为逆变电路提供零电压开关。理论分析和实验结果表明可以实现整个电路的软开关。
2 工作原理分析
    如图1所示，前级电路为全桥移相SPWM控制的 Lcc谐振变换器，其中，S₁、S₂桥臂称为超前桥臂，S₃、S₄桥臂称为滞后桥臂。S₁和S₄驱动信号的上升沿之间夹角q 称为移相角，其大小按照正弦半波规律变化，移相角的变化使得作用在Lcc谐振网络上的输入电压V_AB按照相应规律变化，通过改变调制比的大小来调节输出电压的幅值。中级电路由高频快恢复整流桥将高频变压器输出电压整流成正弦半波包络线，然后通过滤波电感L_d和小电容C_f滤除其高频分量，只剩下低频正弦信号。后级低频逆变器在低频正弦电压信号的过零点，进行开关切换，从而得到期望的低频交流输出，如图2所示。可见后级低频逆变器在ZVS条件下进行开关，而且开关频率低，所以开关损耗极小。

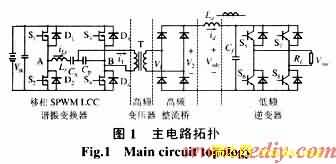
3  控制方法分析
    图3是本文移相SPWM控制的实现方法。其中U_c为三角波载波信号，U_m为正弦半波调制信号。其基本工作过程：载波信号和调制信号进行单极性调制，形成正弦脉宽调制信号U_cmp：当载波信号高于调制信号时，输出低电平；当载波信号低于调制信号时，输出高电平。然后将U_cmp信号的下降沿和上升沿分别作为二分频电路的触发信号，可获得开关管S₁和S₄的驱动信号，根据互补关系获得S₂和S₃的驱动信号。通过检测参考正弦波V_sinref的过零点获得S₅~S₈的驱动信号。

4  稳态分析
    （1）假设滤波电感L_d很大，移相电路的开关频率远大于低频正弦输出频率，则在一个载波信号的开关周期内，整流电流基本不变，即高频变压器原边电流呈阶跃变化形式，如图4所示^[1]。
    （2）开关器件、二极管、谐振电感和电容等元件都是理想的。
    （3）高频变压器分布电容和漏感分别折算到谐振电容C_p和谐振电感L_r中^[5]。
    （4）三次及以上谐波被谐振网络充分滤除，因此谐振网络输入电压用基波分量表示。
    （5）当负载为感性时，将其电感量折算到滤波电感中，只考虑其纯电阻值。
    （6）在任何相邻两个载波周期内，得到U_cmp信号的两个对应脉冲宽度相同。
    文中符号定义参见附录。

       由上述假设可得图1的交流等效电路如图5所示^[6]。 

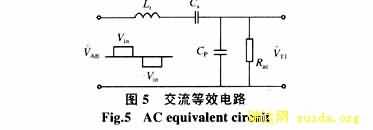
    其中，交流等效电阻R_ac^[6]

    由图5可得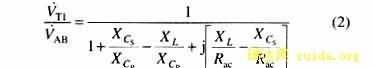

    以任何一个载波信号正峰值对应的时刻作为坐标原点，则由图3可知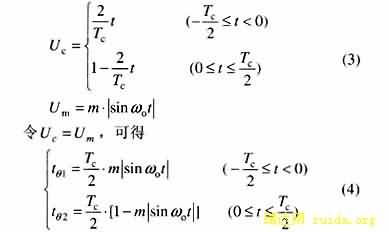

    将图3的V_AB信号变换为图6所示，由于ω_c远大于ω₀，因此该波形近似满足奇函数条件，对该函数进行傅立叶级数分解^[7]。

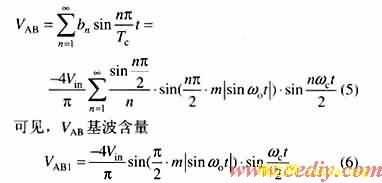
    由式(8)，利用MATLAB软件绘出下列一族曲线，如图7所示。

       由图7可知：随着Q值增加，输出电压下降，因此设计时，应考虑最大负载情况。
    图7(a)表明当f_n在0.5~0.6之间时，输出与负载无关，但此时开关频率低于谐振频率并且输出电压略高于输入电压。
    图7(b)表明当K大于2时，输出与负载无关，图7(c)表明当C_p/C_s约大于4.5时，输出也与负载无关，但此时输出电压都小于输入电压。
    图7(d)表明调制比m较小时（约小于0.5），输出与m基本呈线性关系，当m较大时，输出与m呈非线性关系。
5 实验结果
    根据上述分析可知,虽然该电路作为降压电路可能优于升压电路，但考虑到f_n大于1，因此设计了一台升压原理样机。输入电压V_in=100V ，输出电压V_oac(max)=220V，输出功率120W。所用参数：L_r=240mH，C_s=1.2mF，C_p=0.45mF，f_c=40kHz，f_r=18kHz，K=1/2 ，L_d=5mH，C_f=0.1mF，R_L=200W，L_L=10mH，m=0.5。
    图8(a)表明开关S₁的驱动信号在其反并联二极管续流时有效，所以移相电路超前桥臂为ZVS开通。图8(b)表明开关S₃在接近零电流时关断，而且此时反并联二极管导通，所以滞后桥臂为准ZCZVS关断。

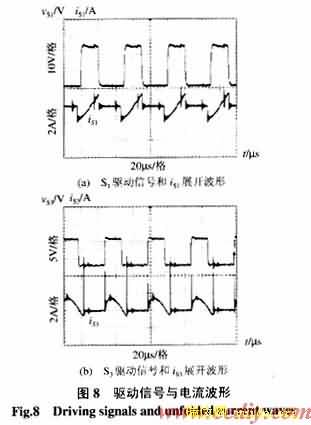
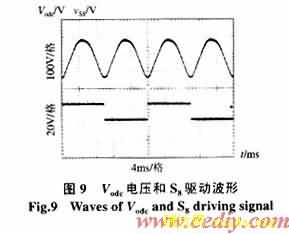
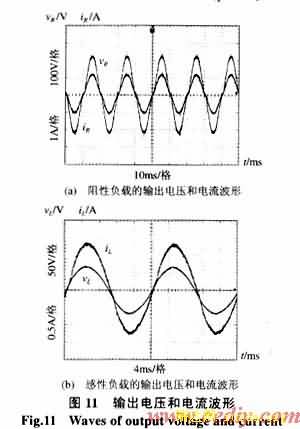
    图9表明低频逆变电路为ZVS开关。图10验证了假设条件的正确性。图11表明对于阻性和感性负载时，该电路是适用的，验证了假设条件的正确性。同时，图11(b)也表明当负载功率因数较低，即Q值较大时，在相同输入直流电压下，输出电压变小。若输出电压保持不变，则可以通过适当减小f_n、K、C_p/C_s以及适当增加m值实现。

6  结论
    （1）通过选择合适的谐振参数、变压器匝比及调制系数，该电路既可以升压，也可以降压。但总体来讲，降压时受负载影响较小。
    （2）移相电路的超前桥臂实现了零电压开通，滞后桥臂实现了准ZCZVS关断。
    （3）低频逆变器实现了零电压开关。
    （4）该电路适用于阻性和感性负载。

参考文献

[1]  Bhat A K S，Dewan S B．DC-to-utility interface using sinewave resonant inverter[J]．IEE Proceedings，1988，135(5)：193-201．
[2]  Rajagopalan V，Rajashekara K S，Al Hadolad K．Analysis and design of a dual series resonant converter for utility interface[J]．IEEE Trans. on Ind. Appl.，1990，26(1)：80-87．
[3]  陈道炼，张友军（Chen Daolian，Zhang Youjun）．单极性移相控制高频脉冲交流环节逆变器研究（Research on uni-polarity phase shifting controlled inverters with high frequency pulse AC link）[J]．中国电机工程学报（Proceedings of the CSEE），2003，23(4)：27-30．
[4]  Koutroulis E，Chatzakis J，Kalaitzakis K，et al．A bidirectional，sinusoidal, high-frequency inverter design[J]．IEE Proc. Electr. Power Appl.，2001，148(4)：315-321．
[5]  孙向东，段龙，钟彦儒，等（Sun Xiangdong，Duan Long，Zhong Yanru，et al）．高压直流LCC谐振变换器的分析与设计（Analysis and design of high voltage DC power supply with LCC resonant circuit）[J]．电工技术学报（Transactions of China electrotechnical society），2002，17(5)：60-64．
[6]  Steigerwald R L．A comparison of half-bridge resonant converter topologies[J]．IEEE Trans. Power Electron.，1988，3(4)：174-182．
[7]  陈国呈．PWM变频调速及软开关电力变换技术[M]．北京：机械工业出版社，2001．

附  录

    符号定义：
    w_o—输出正弦波角频率；
    w_r—谐振角频率；
    i_T—变压器原边电流；
    i_d—滤波电流；
    V_oac(max)—输出正弦波电压峰值；
    w_c—载波角频率；
    T_c—载波周期；
    f_n—载波角频率与谐振角频率之比的二分之一，即w_c/2w_r；
    M—电压转换比，M= V_oac(max) /V_in；
    m—调制比，调制波峰值与载波峰值之比；
    K—高频变压器原边与副边匝比；
    t_q—移相角对应时间（按载波频率计算）；
    Q—品质因数，Q =w_rL_r/R_L。