1 引 言
    近年来，随着对功率电子系统中非线性行为研究的逐步深入，研究人员发现开关式DC-DC变换器是一个强非线性时变动力学系统，具有丰富的非线性行为分岔与混沌。工作在混沌状态的DC-DC变换器，输出特性发生了明显的变化，主要表现为变换器的输出纹波中高次谐波分量的增加，峰峰值加大，以及开关管上的尖峰脉冲幅值的大幅度增加现象。因此，对功率变换器分岔和混沌现象的研究，对于避免、消除和利用混沌具有非常重要的指导意义。
2　理论基础
　　以电压控制型Buck变换器为例对倍周期分岔和混沌进行研究。图1所示是电压控制型Buck变换器的原理图。
　　在连续工作模式（CCM）下，由于线性放大器OA1的增益为A，有：

其中：V_con为控制电压；V₀为输出电压；V_ref为参考电压。
　　当控制电压小于斜坡电压时，功率开关开通，二极管截止（S₁阶段）；反之，当控制电压大于斜坡电压时，功率开关关断，二极管导通（S₂阶段）。

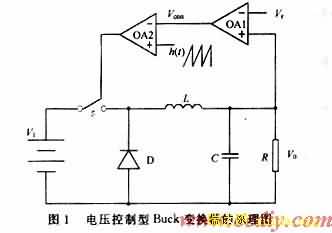
　　令x＝［i_L，v_c］^T为状态变量，i_L为电感电流，v_c为电容电压，v_i为输入电压，v_o为输出电压，则Buck变换器可由下列2个动力学方程来表示。
    S₁阶段的动力学方程为：


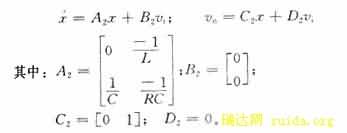
3　Buck变换器中分岔与混沌的仿真和实验
3．1　Buck变换器中分岔与混沌的仿真
　　在这里采用“逆向”分析法来对仿真模型进行分析，即：假设已知Buck变换器的输出特性，“逆向”推出在不同周期解（如周期-1解，周期-2解，…，混沌解等）的状态下所对应的电路参数空间，从而达到研究Buck变换器中混沌特性的目的。
　　从理论角度上讲，任何一个电路参数都可以用作分岔参数来进行讨论，在这里只对输入电压V_i进行改变，从而观察Buck变换器的分岔与混沌现象。
　　对图1使用Matlab中的Simulink进行仿真，将V_i从16 V增至34 V（其他参数如下：L＝20 mH，C＝47μF，R＝22Ω，A＝8．4，V_ref＝11．3 V，V_l＝3．8 V，V_u＝8．2 V，T＝400μs）。在此过程中，Buck变换器经历了周期-1周期-2直至混沌。经仿真发现，Buck变换器的周期轨道稳定性变化如下：
    当V_i＝23．765 V时，发生第1次倍周期分岔；
    当V_i＝27．025 V时，发生第2次倍周期分岔。
　　对于更高的输入电压V_i，变换器将经历不断的倍周期分岔直至混沌。
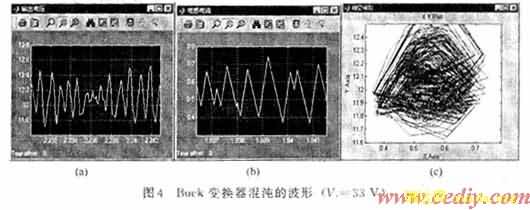
　　当V_i＝32．59 V时，Buck变换器将进入混沌状态。
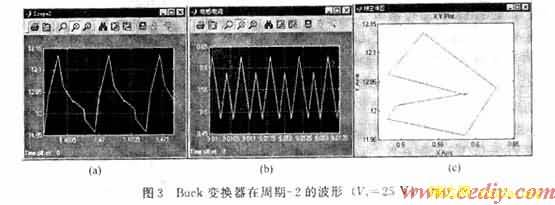
    图2，图3，图4分别为Buck变换器在周期-1、周期-2及混沌的波形。其中（a）为输出电压、（b）为电感电流、（c）为输出电压／电感电流相空间图。

3．2　Buck变换器中分岔与混沌的实验
　　为了验证计算机仿真的正确性，设计了一个电压控制型Buck变换器，以输入电压V_i作为分岔参数进行实验研究，观察到了变换器的输出电压V_o随着输入电压V_i的变化从周期-1的稳态经历倍周期分岔进入混沌的波形。
    图5是电压控制型Buck变换器的实验电路图。

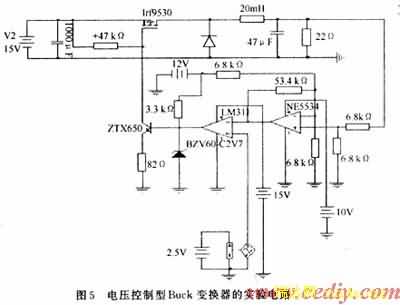
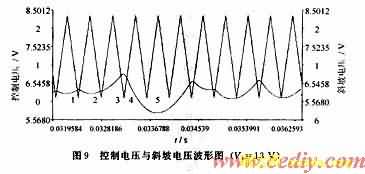
　　图5中IRF9530-P沟道的MOSFET作为功率开关管，NE5534作为误差放大器，LM311作为电压比较器，斜坡信号发生器由555定时器产生。电路的工作过程如下：变换器经过电阻分压器将输出电压送至误差放大器的同相输入端，与参考电压经过比较放大之后，得到误差电压并送至电压比较器的反向输入端，与斜坡电压进行比较。当误差电压大于斜坡电压时，电压比较器的输出为0，ZTX650截止，IRF9530关断，迫使输出电压减小；当误差电压小于斜坡电压时，电压比较器的输出被BZV60-C2V7限制在2．7 V，ZTX650导通，IRF9530闭合，迫使输出电压增加。变换器就是这样不断地跟踪输出电压的变化，调节功率开关管的导通与截止的时间，从而达到稳定输出电压的目的。对于此电路，以输入电压V_i作为分岔参数，令
V_i从13 V增至20 V，步长为1 V，实验结果如表1所示。
    从表1中可以看出，输入电压V_i在14～18 V时变换器稳定在周期-1，当V_i＝19 V时变换器发生第1次倍周期分岔，当V_i＝20 V时变换器发生第2次倍周期分岔，当V_i＝13 V时变换器产生混沌现象，仿真结果与实验结果基本一致，Buck变换器随着输入电压的增长，经历若干次倍周期分岔直至混沌的规律从实验结果中已经得到了体现。
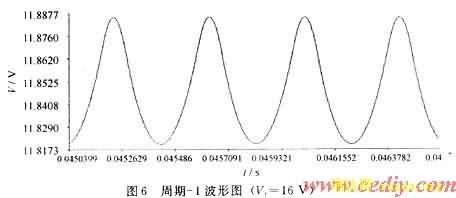
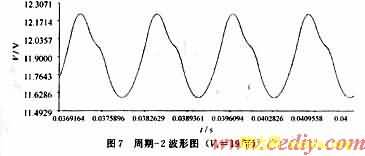
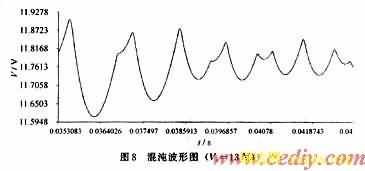
　　图6是输入电压V_i为16 V时输出电压的周期-1波形，周期为400μs，纹波幅值约为65 mV。图7是输入电压V_i为19 V时输出电压的周期-2波形，周期为800μs，纹波幅值约为712 mV。图8是输入电压V_i为13 V时输出电压的混沌波形。

4　结　语
　　基于Buck变换器的仿真模型和实验电路，本文针对输入电压V_i这个分岔参数，分析了Buck变换器的倍周期分岔和混沌现象。仿真与实验结果表明，Buck变换器存在着较大范围的非线性行为，当分岔参数发生变化时，系统就会沿着倍周期轨迹运动，并最终进入混沌。当然不仅输入电压可以作为分岔参数，还有输出的负载电阻参数、电感参数、电容参数、开关管的频率参数等均可作为分岔参数。从以上的分析，得出了一些启示：
　　（1）为了使变换器不会发生混沌或减小混沌发生的可能性，应该尽量使分岔参数远离分岔点；
　　（2）如果能够控制在高输入电压情况下的倍周期分岔，使变换器的输出电压的纹波始终保持周期－1稳态，也就能够提高变换器输入电压的工作范围。