1引言
    数字滤波器在数字信号处理的各种应用中发挥着十分重要的作用。它是通过对采样数据信号进行数学运算处理达到对信号进行处理的目的。数学运算通常有时域和频域两种形式。其中，时域法是对离散采样数据作差分方程数学运算来达到滤波的目的。
    相对于FIR（有限长单位冲激响应）数字滤波器，IIR（无限长单位冲击响应）数字滤波器相位是非线性的，且选择性越好，相位非线性越严重。但是，由于其采用递归型结构，其系统函数的极点可以位于单位圆内的任何地方，因此可用更低的阶数获得更高的选择性，使用更少的存储器。
    数字滤波器一般可以用两种方法来实现：一是采用通用计算机，利用计算机软件通过计算机来实现；二是通过DSP（数字信号处理器），利用为其专门设计的数字乘法器、加法器、存储器等硬件资源，通过处理器的高速运算实现。
2系统硬件介绍
    本系统采用的处理器是得克萨斯仪器公司(TI)的浮点运算DSP——TMS320C31。它采用了并行流水线处理结构，带有硬件乘法器,具有高速并行处理能力、高速浮点乘法及加法运算能力。利用扩展精度浮点格式和寄存器能进行40位浮点运算。TMS320C3X具有丰富的指令集,其3操作数乘法指令、乘加并行指令和零额外开销循环以及延时跳转等指令，非常适合快速实时地完成具有乘加累积求和特点的数字信号处理算法。
    其中，乘加并行指令可以在一个指令周期内同时执行乘法和加法操作。如果该指令中乘法指令的目标地址和加法指令的源地址相同，在进行运算之前，所有的源操作数已被读入，故不会引起源地址与目标地址寄存器的冲突。
    循环寻址模式可以根据程序事先设定的边界地址和需要循环的地址空间长度，在地址指针超过该地址空间的起始边界时，使之自动跳转到其尾部边界；同样，在地址指针超过该地址空间的尾部边界时，自动跳转到其起始边界。其中，起始边界地址（二进制）最低两位应当为零，即该地址应为4的整数倍。
3IIR数字滤波器的级联结构
    假设讨论的IIR系统是因果稳定的。一个IIR数字滤波器级联结构可以用图解，如图1所示。

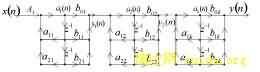
    图中，每个“田”字形环节就是一个二阶子系统。从图中可见，dk(n)可以认为是各二阶子系统输入/输出中间环节，dk(n－1)、dk(n－2)分别是它的延时单元。另外，每个二阶子系统的输出将成为下一个二阶子系统的输入。可以得到IIR数字滤波器的系统函数为：
    （1）
    第k个二阶子系统的差分方程为：
    （2）
    这样，滤波器的系统函数可以通过若干个二阶子系统的级联形式来实现。由于各个二阶子系统在形式上是一样的，这可以使用同一算法，通过改变系数可方便地实现各个二阶子系统，其算法是整个滤波器软件编写的重点。
4IIR数字滤波器在TMS320C31上的实现
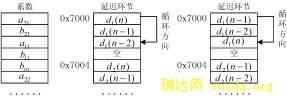
    滤波器程序可以根据其系统函数对应的差分方程实现。对该滤波器在TMS320C31上的资源分配及软件编写如下所述（参见图2）。

IIRmpyf3＊ar0,＊ar1,r0；a21×d1(n－2)，存入R0
mpyf3＊＋＋ar0(1),＊ar1－－(1)％,r1；b21×d1(n－2)，存入R1
mpyf3＊＋＋ar0(1),＊ar1,r0；a11×d1(n－1)，存入R0
||addfr0,r2,r2；a21×d1(n－1)＋x(n)，存入R2
mpyf3＊＋＋ar0(1),＊ar1－－(1)％,r0；b11×d1(n－1)，存入R0
||addf3r0,r2,r2；d1(n)=a21×d1(n－2)＋a11×d1(n－1)＋x(n)，存入R2
mpyf3＊＋＋ar0(1),r2；b01×d1(n)，存入R2
||stfr2,＊ar1－－(1)％；d1(n)的结果存入RAM
rptbfilter；循环执行N>1级的二阶子系统部分
mpyf3＊＋＋ar0(1),＊＋＋ar1(ir0),r0；a2k×dk(n－2)，存入R0
||addf3r0,r2,r2；b1（k－1）×dk－1(n－1)＋b0(k－1)×dk－1(n)，存入R2
mpyf3＊＋＋ar0(1),＊ar1－－(1)％,r1；b2k×dk(n－2)，存入R1
||addf3r1,r2,r2；yk－1=b2(k－1)×dk－1(n－2)＋b1（k－1）×dk－1(n－1)；；＋b0(k－1)×dk－1(n)，结果存入R2
mpyf3＊＋＋ar0(1),＊ar1,r0；a1k×dk(n－1)，存入R0
||addf3r0,r2,r2；a2k×dk(n－2)＋xk(n)，存入R2。其中xk(n)=yk－1
mpyf3＊＋＋ar0(1),＊ar1－－(1)％,r0；b1k×dk(n－1)，存入R0
||addf3r0,r2,r2；dk(n)=a1k×dk(n－1)＋a2k×dk(n－2)＋xk(n)，存入R2
stfr2,＊ar1－－(1)％；dk(n)的结果存入RAM
filter mpyf3 ＊ ＋ ＋ ar0(1), r2,r2 ； b0(k － 1)× dk(n)， 存 入 R2
addf r0,r2 ； b1k× dk(n－ 1)＋ b0(k － 1)× dk(n)
addf3 r1,r2,r0 ； y(n)=b2k× dk(n－ 2)＋ b1k× dk(n－ 1)＋ b0(k － 1)× dk（ n） ，
其 结 果 存 入 R0
nop ＊ ar1－ － (ir1) ；
nop ＊ ar1－ － (1)％ ； 指 针 重 新 指 向 d1(n－ 2)
rets ； 返 回 主 程 序
end
    存储器分配如图2所示。每个二阶子系统对应一个系数数组和延迟环节数组。数组均采用连续地址分配的方法配置存储空间，各系数和延迟单元如图2所示。从（2）式可见，滤波器的每个二阶子系统需要保存的延迟单元包括d(n)，d(n－1)，d(n－2)。可以用最新产生的d(n)替换已经使用过的d(n－2)，以减少存储空间。这可以通过TMS320C31的循环寻址方便地实现。由于循环寻址的边界地址最低两位必须为零，所以每个延迟环节将至少由4个存储单元组成，其中第4个单元可以不使用。图2中第一个延迟环节数组的边界地址为0x7000，第二个为0x7004。
    以下给出的是IIR数字滤波器子程序部分。假设初始化过程中，已经把系数数组的首地址赋予寄存器AR0，延迟环节数组d1(n－2)单元的地址赋予AR1；采样值x(n)通过寄存器R2传递；滤波后的结果y(n)保存在R0中；IR0、IR1寄存器中分别赋值为4（每个延迟数组单元数）和4×(N－1)，用于延迟环节指针的跳转；循环次数计数器RC赋值为N－2；循环寻址块大小为3（字节）。程序中，带有“||”符号的为并行寻址指令，带有“％”符号的为循环寻址指令。
4实验及结果
    确定需要设计的IIR数字滤波器为巴特沃斯低通滤波器，要求3dB处转折频率为800Hz，1200Hz处对1kHz以上频率的信号幅值衰减大于20dB。数据采样频率控制在25kHz。
    利用MATLAB可以方便地确定滤波器的各项系数。得到N=3（六阶），系数b2、b1、b0、a2、a1如表1所示。

表1 IIR低通滤波器系统函数系数表

N	b2	b1	b0	a2	a1
1	0.4619345665	0.9199600816	0.4580365419	－0.8856344820	1.8819136620
2	0.4999946356	0.9999673963	0.4999847412	－0.9149757306	1.9111969789
3	0.4957709610	0.9957589507	0.5	－0.9680170416	1.9641336202

    实验结果如图3和图4所示。图3是输入波形，图4为滤波后的输出波形。

5结论
    本文介绍了IIR数字滤波器的级联结构和它在TMS320C31数字信号处理器上的实现。通过设计不同类型的滤波器参数，可以将该滤波器方便地应用于低通、高通、带通等各种数字滤波器。通过在实际控制器中的应用，显示了较好的性能。

参考文献

[1]程佩青.数字信号处理教程[M].北京：清华大学出版社，1995
[2]蒋静坪.计算机实时控制系统[M].杭州：浙江大学出版社，1992.
[3]王念旭.DSP基础与应用系统设计[M].北京：北京航天航空大学出版社，2001.