高频高压变压器分布电容的分析与处理--打印文章

高频高压变压器分布电容的分析与处理来源于瑞达科技网

作者：佚名文章来源：网络点击数更新时间：2011/1/25 文章录入：瑞达责任编辑：瑞达科技

摘要：本文在分析高频变压器分布参数机理的基础上，以高压直流LCC谐振变换器为实例，阐述了高频高压变压器分布电容对电路带来的不利影响，提出了一种补偿的方法，进行了仿真和实验，提出了高频高压变压器分布电容的测试方法，推导了补偿电感的计算公式，综合使用了两种针对分布电容的处理方法。实验结果表明该方法的正确性。

关键词：分布电容高频变压器 LCC谐振

Analysis and Disposal of Distributed Capacitance in High-Frequency and High-Voltage Transformer

Jin Shun1 ， Zheng Guang1 ，Shi Ming2

（Xi’an University of Technology, Xi’an 710048, China; Xi’an Telecom, Xi’an 710003,China）

Abstract: On the base of analyzing of mechanism of distributed parameters in high frequency transformer, and with a instance of LCC resonant converter , the disadvantage of distributed capacitance in high-frequency and high-voltage transformer is described .A compensation method ,waveforms of both simulation and experiment, and a method of measuring distributed capacitance are given .Formula for calculation compensation inductance is derived .Two methods are used in solving the trouble . Experimental results are presented to verify the theory.

Key words: Distributed Capacitance High Frequency Transformer LCC Resonant

1 前言

随着开关电源频率的不断增加，在满足了减小开关电源体积要求的同时，也带来了一系列新的问题。例如分布参数在高频情况下对电路的影响就不能再被忽略。在开关型电源电路中，高频变压器是电气隔离，传输能量，电压变换的重要元件。在高频情况下，许多应用于工频的变压器设计方法不再适用，考虑及解决好高频变压器的分布参数问题非常重要。

2 高频变压器分布参数模型及对分布参数问题的一般解决办法

文献[1]指出：变压器的分布参数主要是漏感和分布电容。分布电容主要是匝间电容和层间电容。并建立了一个绕组的分布参数模型（图1），再经过叠加折算得到整个变压器的分布参数模型。

由图1a可计算得绕组的等效并联电容。等效电容一般是pF数量级，在工频时可将其忽略，但在高频时其对变压器的影响不容忽视。该分布电容由变压器结构，材料，体积，绕制工艺等因素决定，目前不可能完全消除。

(a) (b)

图1 (a)变压器磁路中的绕组

（b）图1a的等效电路

对待该电容的处理主要有两种方法，一是利用，二是补偿。如果系统需要在变压器端口并联一个电容，正好可以利用分布电容作为该并联电容，不仅解决了分布电容带来的危害，还减少了元器件的数量。这是最为积极有效的办法。反之，若在变压器端口并联电容会给系统带来危害，则必须减弱其影响。主要是通过工艺上的改进和在变压器外部对其进行补偿。下面通过工程中实例——高压直流LCC谐振变换器，详细阐述两种方法的应用。

3 LCC主电路原理介绍

该电源输入工频220V电源，输出直流电压0~10000V,输出最大功率500W。主电路（图2）由两级变换电路组成，前级为Buck降压电路，用来实现稳压目的。后级为LCC谐振电路，为开关器件提供零电压开通条件，变压器副边采用高压硅堆整流，输出为10kV。

通过对LCC谐振电路的详细分析，由电路工作于主模式的状态轨迹图，推导出其稳态时的解析表达式，根据此解析表达式画出LCC谐振电路的负载曲线。最后，根据此曲线设计了实验参数：

，，。设计电路稳态时，工作于如下状态：开关频率为20KHz，T=50μs，输出功率500W，输出电压10kV。高压变压器变比为1：100，则变压器原边的电压为100V，Io为5A。

4 实验波形及结果分析

实验中，负载为200k电阻，输出负载电压为10kV。图3（a）中，通道1为开关管上的电压波形VCE=2VS，大约160V，通道2为谐振电感电流波形，峰值大约20A。图3（b）为谐振电容C2上的电压波形。图3（c）为输出负载部分电压，等于总电压的二十分之一。实测效率约为90%，这主要由于BUCK调压电路开关损耗较大。

（c）输出负载部分电压

图3 实验波形

从实验波形上看，基本与理论分析一致，输出电压也能够达到10000V，系统能够按设定工作。但是，在持续工作一段时间后发现谐振电感L发热严重，主谐振电流开始不稳定，噪声加大，系统不能正常工作。由于在一段时间内系统能够正常工作，说明电路原理没有问题。又鉴于故障发生总是在半小时左右，初步断定故障是由L发热引起。由图3a可见流过L的主谐振电流峰值为20A，这比设计值10A大了一倍。输出一万伏直流电压加在200K电阻负载上消耗500W功率没有问题，变压器副边高压滤波整流模块亦没有发热现象。测量变压器原边输入电流峰值为19A左右，远超过设计值。说明问题出在变压器上。对该1：100变压器进行空载试验，输入20KHz交流，发现空载电流非常大，且电流超前电压90度，似乎该变压器带了一个电容负载。

5 分布电容的测量及仿真验证

考虑到前述的高频变压器绕组分布参数模型，建立图4所示的高频变压器模型。

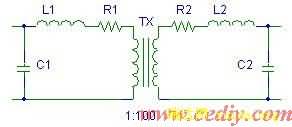(a)高频变压器模型

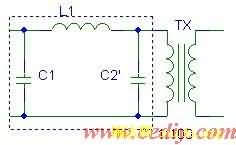
(b)高频变压器简化模型

图4 高频变压器分布参数模型及简化

其中L1，L2分别为原边和副边的漏电感；C1为原边绕组等效分布电容，C2为副边绕组等效分布电容；R1，R2分别为原边和副边绕组的电阻；Tx为没有分布参数的理想铁氧体铁心变压器。考虑到副边电流很小，R2，L2可忽略不计。而原边只有几匝，R1亦忽略不计。再将C2折算到原边后得到图4a的简化模型(图4b)。考虑到副边匝数是原边匝数的100倍，且绕制工艺一样，可以得到。将C2折算至原边后,有：

将图4b虚线框内的型双端口网络等值为T型双端口网络（图5a）。又由于Tx励磁电抗很大，励磁电流忽略不计，空载时图5a可等效为图5b。

(a) T型双端口网络

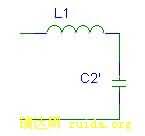
(b) 空载等效电路

图5 分布参数模型的等效简化

图5b中串联阻抗，因为 <<1，所以。给图5b端口加上20KHz正弦激励，测量输入电压和电流，可算出：

，

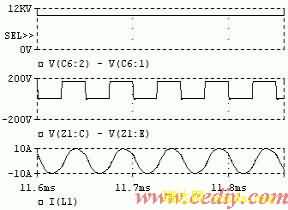
把此分布电容并联到变压器副边端口，用Pspice仿真软件进行仿真。其结果(图6a)与不考虑分布电容的仿真结果(图6b)进行比较可以看出：主谐振电流分别为峰值20A和10A左右，分别与实验和理论值相符合。说明上述分布模型以及分布电容的计算是比较准确的。

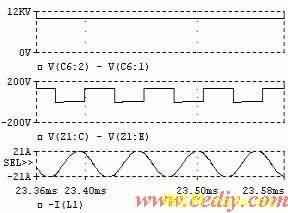（a）考虑分布电容的仿真波形

（b）未考虑分布电容的仿真波形

图6 仿真波形（依次为：输出电压，

开关管压降，主谐振电流）

6 分布电容解决方案

解决该分布电容对系统的不利影响，可从两方面着手：1.利用 2.补偿。考虑到主电路正好需要与该主变压器原边端口并联一个0.2uF的电容，而由以上分析可知分布电容折合到原边相当于在原边并联了一个1uF左右的电容，因此可去掉原电路中0.2uF的电容，利用1uF的分布电容代替。然而1uF电容比期望的0.2uF大得多，因此需要进一步采取措施减小分布电容。这可以从两个途径来着手。一是改进变压器的绕制工艺，一是用外部并联电感进行补偿。在多次改进工艺效果不明显的情况下，采用第二种方法。下面就补偿法详细介绍。

在图5a虚线框左端口并联电感L*，得到电路图7a。

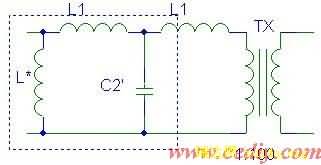(a)加电感补偿后的电路

（b）a图虚框内的T型等值电路

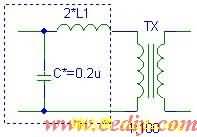
（c） b图虚框内的等效简化电路

图7 电感补偿电路的分析简化

图7a虚线框内的型双端口网络可以等效为图7b虚线框内的T型双端口网络。其中：（式1），。现令C*=0.2uF，得L*=0.08mH，再将L*代入式1，并考虑到L1和C2’数量级都是，Z1相当于是一个相当大的电容，对于20KHz来说Z1相当于短路。因此，可得到图7c的简化等效电路。从图7c可以明显的看出，经过L*补偿以后，原来的变压器相当于漏感加大了一倍，并在原边并联了一个0.2uF的电容，正好符合主谐振电路的参数要求。当然也可以在变压器副边并联补偿电感，但考虑到副边电压非常高，电感体积很大以及制作调试困难而不予采用。