 打印本文
打印本文  关闭窗口
关闭窗口 摘 要:本文推导了三相变流器在旋转坐标系下的数学模型,在此基础上,又进一步分析了三相四开关工作模式的数学模型和三相电压不平衡时的控制方法,本文提出了采用负载电流前馈的方法以加快系统的动态响应,并给出了相应的仿真结果
关键词:三相变流器 四开关 前馈控制 功率因数
Abstract:In this paper, a mathematical model of three-phase voltage source converter was first derived in the stationary and synchronous reference frames. Secondly, modeled the three-phase four-active-switch voltage source converter and the control law to handle the effect of unbalanced input voltage was analyzed. Then, a load current feed-forward control was used to improve the transient performance of three-phase voltage source converter. Finally, the simulation results were given.
Key words: three-phase voltage source converter four-active-switch feed-forward control power factor
1 引 言
随着电力电子技术的发展,AC/DC变流器在各个领域得到广泛的应用。全控型高频PWM变流器具有输出直流纹波小,网侧功率因数高甚至可调,以及能量可以双向流动的特点而得到人们的重视,成为研究的热点。
从控制方式上看,PWM变流器通常可以分为直接电流控制[1][2][3]和间接电流控制[4][5]。直接电流控制的优点是动态响应好,但是需要频带比较宽的电流传感器。间接电流控制动态响应慢,而且会有直流分量。
本文在dq变换的基础上,得到了电压型三相变流器的开环数学模型。在不使用电流传感器的情况下,使PWM变流器仍可工作在单位功率因数下。然后又分析了在四开关模式下的工作情况和三相电压不平衡时的工作情况,并给出了相应的仿真结果。
2 数学模型

图1 三相变流器主电路拓扑
首先假定三相电压平衡,可以得到一般数学模型
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() 为整流桥和电感的等效阻抗
为整流桥和电感的等效阻抗
![]() (4)
(4)
![]()
![]()
k=1,2,3 (5)
占空比与调制函数的关系是
![]() (6)
(6)
首先定义三个空间矢量
 (7)
(7)
其中,
 (8)
(8)
将式(7)(8)代入三相变流器的数学模型中,可以求出

![]() (9)
(9)
可以看出,按照上式进行调制, ![]() 就可
就可
以自动的被控制,而不用电流传感器。
3 四开关SPWM技术
传统的全桥整流器在其中一个桥臂出现故障时,并不能正常的工作,为了加强系统的鲁棒性,使用四开关的工作模式[6]。当某一个桥臂发生故障时,封锁这个桥臂的门极触发信号,然后把该桥臂的跳线联结到两个电容中间,这样只剩下四个开关被控制。为了便于说明,假设第三相桥臂出现故障,它的电路拓扑如图2所示。

图2 四开关模式电路拓扑
从电路拓扑上可以得到它的数学模型
 (10)
(10)
 (11)
(11)
 (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
从数学模型中得出稳态解
 (15)
(15)

(16)
![]() (17)
(17)
这样,不用电流传感器也可以自动的控制电流,并且可以保证输出电压的恒定和系统的功率因数可调。这无疑增加了系统的鲁棒性。当其它桥臂故障时,推导方法类似。
4 电压不平衡时的调制方法
电压不平衡是整流器经常遇到的工作情况,当三相电压不平衡时,可以将其分解为正序分量和负序分量[7]。
假设三相不平衡电压为

![]() (18)
(18)
将上式dq分解
 (19)
(19)
 (20)
(20)

(21)

(22)
假设三相不平衡电流为
 (23)
(23)
把上式分解
 (24)
(24)
 (25)
(25)
 (26)
(26)
 (27)
(27)
与第一部分的推导方法类似,可以得出三相电压不平衡时的调制函数与输出电压的稳态解。
 (28)
(28)
![]() (29)
(29)
 (30)
(30)
![]() (31)
(31)
 (32)
(32)
 (33)
(33)
考虑到一般情况下,相角的波动很小,并且系统一般都工作在单位功率因数下,有
![]() (34)
(34)
 (35)
(35)
 (36)
(36)
期望得到纯直流电压,因此
令 ![]() ,得
,得
 (37)
(37)
 (38)
(38)
 (39)
(39)
这样只要已知三相电压的峰值和PI调节器的输出电流,就可以得出工作在单位功率因数下的调制函数。在这种情况下,尽管三相电压不平衡,仍可以使系统工作在单位功率因数下。
5 仿真波形
在仿真中,使用负载电流前馈控制以减少负载扰动,加快系统的动态响应速度[8]。
仿真参数如下:

电压不平衡时的参数为
![]()
负载前馈比例系数K=6.6
PI调节器为 ![]() 。
。
仿真波形如图所示
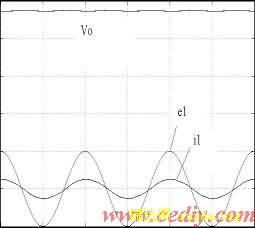
图3 四开关工作模式下 ![]() 与
与 ![]() (50V/div)
(50V/div)
如图所示,直流输出电压稳定,输入电压和输入电流保持同相位。
![]()
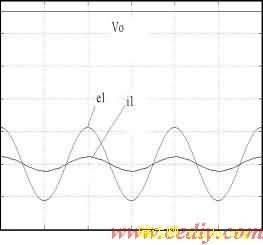
图4 三相电压不平衡时的 ![]() 与
与 ![]() (50V/div)
(50V/div)
如图所示,直流输出电压稳定,系统工作在单位功率因数情况下。
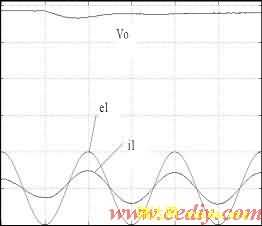
图5 加入负载电流前馈时的负载扰动波形(50V/div)
如图所示,当负载扰动时,在两个工频周期内可以达到稳定,并且没有直流分量。
6 结 论
本文首先推导出三相变流器的数学模型,得出三相变流器正常工作情况下的调制函数。其次,推导出四开关模式的数学模型,得出四开关模式下的调制函数,使系统的鲁棒性得以加强。在dq分解的基础上,又推导出输入电压不平衡时的调制函数,使变流器在电压不平衡时可以工作在单位功率因数下。以上三种工作模式,系统都可以在不使用电流传感器的情况下,达到正弦电流输入,输出电压可调,功率因数可调,能量可以双向流动的性能要求。最后,提出使用负载电流前馈的方法以加快系统的动态响应。并给出以上几种情况相应的仿真波形。
参考文献:
[1] A.W.Green and J.T. Boys “Hysteries Current-Forced Three-Phase Voltage-Sourced Reversible Rectifier “ IEEE proc. Vol.136 Pt. B. No.3 112-120 May 1989.
[2] Rusong Wu etc, “Analysis of a PWM ac to dc Voltage Source Converter under the Predicted current control with a Fixed switching Frequency” IEEE Trans. On IA 1991. Vol.27 No.4 :756-764.
[3] Zargari N R etc. Performance Investigation of a Current-Controlled Voltage-Regulated PWM Rectifier in Rotating and Stationary Frames. IEEE Trans. on Ind. 1995.4 (42) :396-401.
[4] J.W. Dixon and B.T.Ooi “Indirect Current Control of A Unity Power Factor Sinusoidal Current Boost Type Three Phase Rectifier” IEEE Trans on IE Vol.35 No.4 508-515 Nov. 1988.
[5] Rusong Wu etc, “Analysis of an ac-to-dc Voltage Source converter Using PWM with Phase and Amplitude Control” IEEE Trans. On IA 1991 Vol.27 No. 2.355-363
[6] .Shieh J J,pan C T. Modeling and Design of a reversible three-phase switching mode rectifier, IEE Proc.Electr Power Appl,1997,
144:389-396
[7] 张桂斌,徐政,王广柱。“基于空间矢的基波正序、负序分量及谐波分量的实时检测方法.” 中国电机工程学报,第21卷第10期,2001年10月
[8] S. Hiti and D. Botojevich,” Control of front end three phase boost rectifier.” Proc. IEEE APEC 94.pp.937-933.1994
 打印本文
打印本文  关闭窗口
关闭窗口