 打印本文
打印本文  关闭窗口
关闭窗口 关键词: 变压器保护; 误动和拒动; 多原理; 冗余; 可靠性和灵敏性
Applications of Digital Transformer Protection Based on Much Theory
ZHAO Yongbin, CHEN Xiaoyan
(Guodian Nanjing Automation Co,.Ltd, Nanjing 210003, China)
Abstract: The article analyzes application of transformer protection based on different theories, and brings forward much theory's digital transformer protection, theorie s with different advantages and disadvantages are used together in the same prot ection,the protection adopts hardware and software's redundancy, which improves reliability and sensitivity of the protection.
Key words: transformer protection; mistake action and rejec ting action; much theory; redundancy; reliability and sensitivity
1前言
国内微机变压器保护应用越来越广泛,变压器保护的技术难点在于空投变压器的励磁涌流制动。国内外微机保护的涌流谐波制动原理虽已得到普遍应用,但实际应用效果并不理想。每一种保护原理都可以从其数学分析或实际应用中找到它的不足之处。本文从数学方面分析变压器保护的多种原理,然后将不同原理应用在一起,互相弥补各自的不足,设计出一种多原理的微机变压器保护,大大提高了应用的可靠性。
2变压器励磁涌流的特点
正常运行情况下变压器工作在磁通的线性段OS,如图1。铁芯未饱和,其相对导磁率μ很大,变压器绕组的励磁电感也很大,因而励磁电流很小。


当变压器空投或故障切除后电压恢复时,一旦铁芯饱和后,相对导磁率接近1,变压器绕组电感降低,伴随出现数值很大的励磁涌流,其数值可以达到额定电流的6~8倍以上,出现尖顶形状的励磁涌流,如图2。其中含有相当成分的周期分量和高次谐波分量,尤以二次谐波比例较大[1],并且在最初几个周期内可能完全偏于时间轴的一侧,波形出现间断,不对称,此电流流入差动继电器,可能引起保护装置误动。
3励磁涌流的数学分析
假定变压器在电压过零点时投入,分析单相达到的最大总磁通Φ=f(t)的关系,如图3。
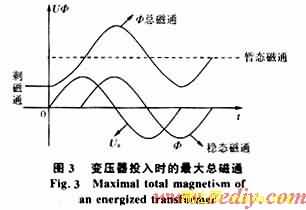
为了分析方便,用两段折线Oa、ab代替磁通曲线Φ=f(I),可分析出电流I=f(t)的关系,如图4,可知电流波形出现间断,间断角为t2<t<t3的角度。
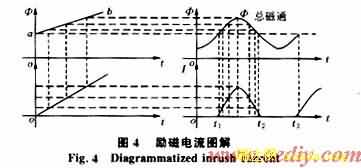
对于单相变压器,忽略回路中的电阻,变压器投入时其暂态过程可用下式表达[1]
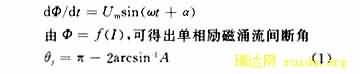

Aa、Ab含义如式(2)所示
A=cosα-(Bs-Br)/(U*Bm)
(2)
其中:
Bs—变压器饱和磁通密度
Br—变压器剩余磁通密度
Bm—变压器最大工作磁通密度
Bm=
U*—空投前系统电压与额定电压之比
假定剩磁:Bra=Brb=Brc=0.6U*Bm,取饱和Bs=1.3U*Bm,则此时流入继电器电流间断角为:θja=θjc=115°,θjb=84°,θjb为对称性涌流的最小间断角。
利用上述关系可求出在不同Bs、Br情况下的间断角。例如,考虑最大剩磁情况,取Bra=Brb=Brc=0.9U*Bm,同时取Bs=1.4U*Bm,利用上述关系可以求得:θjb=π/3,θja=θjc=π/2。如果选取适当的Bs和Br值,最小间断角可能小于30°。
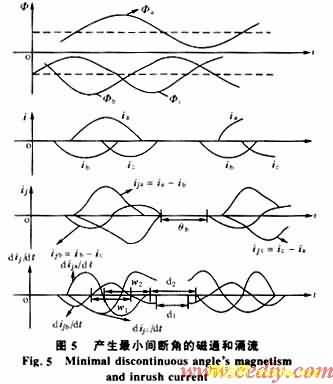
根据运行和动模录波的结果,结合理论分析,一般情况下,间断角θj∈(60°,150°)。
4二次谐波制动原理
变压器空投或切除后恢复供电时,三相励磁涌流中不同程度含有二次谐波分量[1,2],二次谐波分量的含量存在很大的分散性。
为了在变压器空投时保护不误动,常选取三相电流中最大二次谐波含量来闭锁差动保护,即“或”门方式。制动关系如下
max(I2A/I1A,I2B/I1B,I2C/I1C)≥K1
(3)
其中:I1A、I1B、I1C,I2A、I2B、I2C分别表示三相差流有效值和二次谐波有效值。
试验与分析表明:三相中总有一相的二次谐波含量超过30%,一般选取15%~20%的比值便可以很好地闭锁差动保护。所以采用式(3)三相中最大相来制动,可以在变压器空投或故障切除 后恢复供电时可靠闭锁差动保护,保护不误动,这种方法是可行的。但采用式(3)制动方式,如果在带有匝间短路的变压器合闸时,由于变压器容量、电压等级、变压器的铁芯结构等因素影响,励磁涌流可能长达5s才衰减,保护只有非故障相涌流经过长时间衰减后,才能动作[3]。此时可能造成变压器保护的实际拒动,严重时可能烧毁变压器。为了提高此时差动保护的灵敏性,不少人员采用二次谐波的分相制动原理,即“与”门方式,制动关系如下
式(4)中的变量含义如式(3)示。
此时K2取值为7%~12%左右,任何一相的二次谐波含量小于式(4)中的K2值,保护不被谐波闭锁。该原理的二次谐波制动关系在变压器空投或故障切除后恢复供电时,发生轻微匝间故障,涌流闭锁基本上不受健全相的涌流影响,在经过1~2个周波后,保护被解除闭锁,可以快速动作,事故不至于扩大,如图6所示。
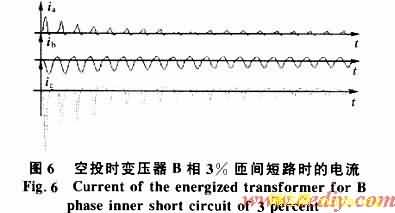
采用式(4)的制动原理,试验分析表明,在变压器空投或故障切除后恢复供电时,容易误动。同样容量、电压等级的变压器多次试验,三相励磁涌流二次谐波含量存在很大的分散性,有时某相的二次谐波含量可能小于7.5%,甚至更小,所以式(4)中的K2值选取即使很小,达到7.5%,也不能可靠的闭锁保护。同时由于电力系统高压超高压长线路以及电缆的使用,补偿电容或电缆容性电流的影响,在正常故障时,也会使故障电流中出现不同含量的二次谐波,如果式(4)中的K2值太小,会在区内故障时误闭锁差动保护,造成保护的 延缓动作或拒动。
针对上述两种二次谐波的选取,式(3)不会造成空投变压器保护的误动,但会在某些故障下,保护延缓动作,式(4)会造成保护的误动和拒动。
5间断角原理
由数学和录波分析可知,涌流波形出现间断,正常情况下间断角θj∈(60°,150°),当 剩磁在0.3~0.7Bm的情况下,利用判断间断角的大小来闭锁差动保护,便可防止变压 器空投或切除后恢复供电时保护误动。为了使允许的最大剩磁达到0.7Bm以上,以及在变压器过激磁时不会误动作,通常增加测量涌流波宽作为判据。
涌流判据取决于涌流导数的最大波宽和最小间断角,在同样饱和磁通密度Bs下,跟剩磁密度Br有很大关系。
1)可能的最大剩磁密度为0.9Bm
波宽θω≥130°,间断角θj≤50°
2)可能的最大剩磁密度为0.3~0.7Bm
波宽θω≥140°,间断角θj≤65°
上述两种情况下的判据,在波宽和间断角同时满足的情况下,方允许继电器动作。
由图5的三相励磁涌流求导可得,此时A相的初相角αa=0,B相励磁涌流ijb为对称性。B相最大波宽θbw=2π/3
A、C相的涌流偏于时间轴的一侧,其导数dija/dt的后半波和dijc/dt的前半波有最大波宽,A相最大波宽θaw=2π/3+arcsinAa,C相最大波宽计算与A相类似。
涌流闭锁元件的波宽和间断角,通常按式(5)整定,波宽θω≥120°,间断角θj≤60°(5)在涌流情况下不满足式(5),闭锁保护;在故障时满足条件,开放保护。
励磁涌流很大时,如果电流互感器饱和,在间断角中会出现反向电流,为防止反向电流影响波宽和间断角,实际计算时取一定的门槛,门槛公式为
IT=K1*iT+I0
其中:
IT代表某相间断角无流时浮动门坎值;
iT为一周内差流的最大值;
K1是比例系数;
I0为门坎值的固定部分。
按此判据的间断角原理保护,可以有效防止变压器空投或切除故障恢复供电后的误动作,但在实际运行时存在一定的困难,现代变压器的铁芯结构和材料的不同,致使每一台变压器的饱和密度Bs、变压器剩磁密度Br不同。由数学分析可知,在相同的Bs下,Br越大间断角越小,波宽越大。在相同的Br下,Bs越大波宽越小,间断角越大。所以在选取波宽和间断角的定值时,存在较大的分散性,通常按式(5)选取也不能反映各种情况下的涌流关系。
就理论分析而言,上述关系在某些条件下是不满足的,仍然存在缺陷:
1)如果间断角取得太小,波宽取得太大,必然会造成区内故障时,误闭锁差动保护,造成保护的拒动或延缓动作。相反,间断角太大,波宽太小,会造成保护误动作。
2)就目前使用的一次普通CT而言,考虑到CT的暂态特性对涌流的传变影响很大,势必会影响式(5)的准确性。
所以间断角的应用同样受到不利因素的影响,同二次谐波制动原理相比,有优势的地方,也有不足之处,但并不否定间断角原理的应用。
6波形对称原理
工作原理是采用一种波形对称算法[4],将变压器在合闸时的励磁涌流和故障时的故障电流区分开来。具体方法是先将流入继电器的差动电流进行求导,在任何时刻t将求导后的前半波和后半波作对称比较,具体关系如下
式(6)中,T表示采样周期。
满足上述关系,波形对称,不满足上述关系,波形不对称,从某一时刻t起连续比较半个周 波,对于故障电流,式(6)恒成立。
对于励磁涌流,由前面分析可知,波形出现不同程度的间断,通常情况下波形间断角大于90 °,所以在比较180°的范围内,至少有一半的电流不满足上述关系。据此关系可以区分变 压器的励磁涌流和故障电流。
但对称原理仍然有不足之处:
1)K值的选择,存在较大的分散性,对于标准的正弦变化量,K值取1左右,但是故障电流同 样含有很多的高频分量和非周期分量,即使滤除部分非周期分量和高频分量,故障电流波形仍然可能不对称于时间轴,前后半波仍然存在不对称性,不对称程度可能达到0.6以下,所以在选择K值时,为了确保区内故障不误闭锁,K值范围通常取0.6~0.9。
2)分析可知,励磁涌流波形的复杂性,可能出现间断或偏向时间轴的一侧,可能对称于时间轴,间断角小于30°,直接影响波形的对称程度,如果K值选取太小,势必造成变压器空投的误动。
3)在实际的运行试验中,故障电流至少有30°是不对称的,150°范围是对称的,在极少数 情况下,甚至可能不满足上述范围。励磁涌流的间断范围通常是60°~120°,如果变压器的剩磁很大,可能使间断角小于60°。经理论计算,在Bs一定的情况下,Br大于0.9倍以上,间断角会达到30°左右,实际录波的结果,波形根本未间断,此时的波形对称程度很强,势必引起误判。
4)在间断角很小的情况下,电流互感器CT的暂态特性,因涌流作用饱和,产生反向电流,反向电流的大小因涌流大小而变化,这样直接影响其对称程度,势必引起误判。由于实际运行时很少出现极端情况,所以波形对称原理仍具有实用性。
波形对称原理与间断角原理本质上是一样的,都是利用涌流波形固有的一些特点,与故障电流加以区别,这两种原理的应用需要较高的硬件支持。对间断角原理要求每周波采样点数不能太低,至少每隔3°~5°采样一点,即要求采样率达到每周波72~120点,计算才够精确。波形对称原理同样因为求导的关系,采样点随求导方式不同,而有不同要求,若电流求导后接入继电器,每周采样点大于24点即可,若由软件计算求导,为了保证求导的精确性,采样点与间断角原理需求基本一致。
7三原理的综合使用
波形对称原理,是反映波形的对称度,即反映波形与坐标轴的偏离程度或间断程度,即相对称对应的每一点大小不一致(包含涌流波形的间断点)。间断角原理是反映波形的间断程度,即在坐标轴上一个周波内有多少点的数值小于某个值,而其余点都大于某个值。二次谐波原理是利用波形所含有的数学特征,即波形的对称度、间断角,直接影响其二次谐波含量。反之,则不一定成立,即有二次谐波含量,并非是涌流波形使然。
所以利用三种原理各自反映的内涵不一样,将三种原理(即数学处理方法)应用在一起,从不同角度、不同方面反映同一问题,便能很好地应用于变压器保护,具体实现方法如下:
用三块CPU板完成这种混合原理的保护,每一块CPU板包含一片DSP和CPU,完成一种原理,独立高性能的数字信号处理器DSP,实现数据采集和计算,高性能的C PU完成保护逻辑设置和通讯功能,其中任何一块原理CPU动作,发相应出口接点。然后硬件采用三取二的组合逻辑出口方式,具体关系如图7所示。
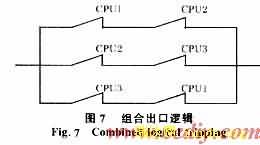
上述三种原理的逻辑,任何两个满足要求,即发出口命令。此种出口逻辑,具有如下优点:
1)在硬件的设置上增加冗余度,不会因任一硬件的损坏,而造成保护的误动。
2)综合利用三种原理的优缺点,可以灵敏、可靠地起到保护变压器的作用。
具体分析如下:
1)变压器空载合闸时,三种原理均可以可靠制动,一般情况下按式(3)、式(5)、式(6)的定值整定,可以起到保护作用。考虑到变压器剩磁的大小存在分散性,以及极不利的情况存在,当间断角很小,波宽较大,或波形的对称程度高,可能造成误动。但在整定波宽、间断角、对称程度为定值时,可以确保其中两个不动作,按以上出口逻辑,保护不会出口。
2)变压器空载合于匝间短路,如果短路匝比较大,短路电流很大。由于故障相的电流不间断,间断角原理和波形对称原理均可以可靠动作,“或门”制动二次谐波原理可能拒动,但仍不影响保护出口。如果短路匝比比较小(小于3%),如图3的B相故障,故障电流很小,此时“或门”制动的二次谐波会拒动,间断角或波形对称原理的保护可能延缓动作,要在1~2个周波后才会动作[3]。因为在合闸的前几个周波,故障相的涌流和故障电流叠加,表现为涌流特征,但1~2个周波内,因为故障点的存在,故障电流的特征表现明显,一般情况下保护会在2个周波后动作,当短路匝比很小(小于1%),保护可能会延缓更长的时间动作。
3)如果某相谐波很小,或间断角很小,此时“或门”制动二次谐波原理不出口,波形对称原理不出口,间断角原理失效,但仍保证了空投保护不误动。故障时,可能故障相谐波很小,“或门”制动二次谐波原理拒动,但波形对称原理和间断角原理,仍保证保护可靠动作。
4)变压器空投于内部接地故障、相间故障等,上述三种原理均可以在很短的时间内出口。
5)无论发生变压器的区内或区外动作,在CT没有饱和的情况下,由于故障电流的明显特征,三种原理中至少有两种可以可靠动作。一般情况下的CT饱和都很容易判别,当区外故障CT饱和时,间断角和波形对称原理还有助于制动,设置差动速断,可以在短路差电流很大的情况下,不经闭锁直接出口。
8结论
电流波形是对变压器特定运行工况的综合反映,分析波形是抓住较为原始的特征,往往是比较接近真实的。二次谐波制动原理的变压器保护,是对电流波形的抽象数学处理,经过长时间的现场运行,绝大部分情况下是可以很好运行的。在大型变压器上综合运用不同保护原理上的先进性,具有很好的应用前景,并具有较高的可靠性。现代的继电保护多以快速的数字处理CPU构成,计算分析方便,容易实现,并且功能愈来愈强大,可以完成老式保护无 法完成的数学功能。
参考文献
[1]王维俭.电气主设备继电保护原理与运行[M].北京:中国电力出版社,1996
[2]贺家李,宋从矩.电力系统继电保护原理[M].北京:水利电力出版社,1994
[3]周泽昕,邱宇峰.从动模试验情况看微机型发电机变压器保护的现状及存在的问题[J].继电器,2000,28(7):45-49
[4]孙志杰,陈云仑.波形对称原理的变压器差动保护[J].电力系统自动化,1 996,20(4):42-46
[5]赵永彬,卢毅.基于样波分析的变压器励磁涌流判别[J].电力系统及其自动化学报,2002,14(5):44-47
 打印本文
打印本文  关闭窗口
关闭窗口