 打印本文
打印本文  关闭窗口
关闭窗口 关键字 数字下变频;CORDIC;FPGA
1 引言
软件无线电的设计思想之一是将A/D 转换器尽可能靠近天线,即把A/D从基带移到中频甚至射频,把接收到的模拟信号尽早数字化。由于数字信号处理器(DSP)的处理速度有限,往往难以对 A/D采样得到的高速率数字信号直接进行各种类别的实时处理。为了解决这一矛盾,需要采用数字下变频(DDC)技术,将采样得到的高速率信号变成低速率基带信号,以便进行下一步的信号处理。数字下变频技术在软件无线电和各类数字化接收机中得到了广泛应用。因此建立软件无线电的通用数字下变频器是非常必要的。
2 下变频器的结构与组成
我们要设计数字下变频器如图1所示。
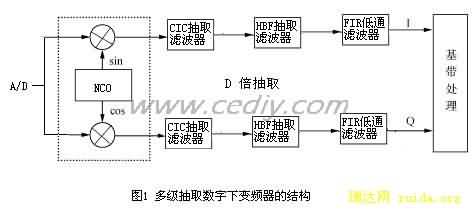 |
量化的中频数字信号进入数字下变频器后,先与数字控制振荡器产生的本地数字载波混频,经过CIC抽取滤波器,HBF抽取滤波器,FIR低通滤波对信号进行D倍抽取后得到正交基带信号,这是下变频过程。虚线框内为数字下变频部分是我们设计和讨论的重点。
3 数字控制振荡器振荡器
如图1所示。正交数字下变频器前端包括两部分一是乘法器;一是NCO。乘法器设计很简单,NCO的目标是产生一个理想的正弦和余弦波。更确切地说是产生一个可变频率的正弦波样本如公式: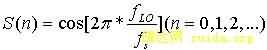 其中
其中 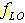 为本地振荡频率;
为本地振荡频率; 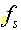 为DDC输入信号的采样频率。正弦波样木可以用实时计算的方法产生,但这只适用信号采样频率很低的情况。在软件无线电高速信号采样频率的情况下,NCO实时计算的方法是不可取的。NCO产生正弦波样本通常采用查表法,通过输入的相位数据来寻址查表输出相应的正弦波幅值。对于一个相位位数为n,输出信号幅度位数为M的数控振荡器,这就需要耗费大量的ROM资源(2nX Mbit)。为了避免使用大容量的存储器。可采用了一种基于CORDIC( Coordinate Rotation Digital Computer)算法来产生正/余弦样本。该算法有线性的收敛域和序列特性。只要迭代次数足够,即可保证结果有足够的精度。并且用于混频的乘法器也可以省掉。从而还节省了大量的逻辑硬件资源。使得数字下变频更易于用FPGA来实现。
为DDC输入信号的采样频率。正弦波样木可以用实时计算的方法产生,但这只适用信号采样频率很低的情况。在软件无线电高速信号采样频率的情况下,NCO实时计算的方法是不可取的。NCO产生正弦波样本通常采用查表法,通过输入的相位数据来寻址查表输出相应的正弦波幅值。对于一个相位位数为n,输出信号幅度位数为M的数控振荡器,这就需要耗费大量的ROM资源(2nX Mbit)。为了避免使用大容量的存储器。可采用了一种基于CORDIC( Coordinate Rotation Digital Computer)算法来产生正/余弦样本。该算法有线性的收敛域和序列特性。只要迭代次数足够,即可保证结果有足够的精度。并且用于混频的乘法器也可以省掉。从而还节省了大量的逻辑硬件资源。使得数字下变频更易于用FPGA来实现。
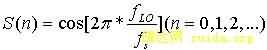 其中
其中 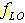 为本地振荡频率;
为本地振荡频率; 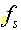 为DDC输入信号的采样频率。正弦波样木可以用实时计算的方法产生,但这只适用信号采样频率很低的情况。在软件无线电高速信号采样频率的情况下,NCO实时计算的方法是不可取的。NCO产生正弦波样本通常采用查表法,通过输入的相位数据来寻址查表输出相应的正弦波幅值。对于一个相位位数为n,输出信号幅度位数为M的数控振荡器,这就需要耗费大量的ROM资源(2nX Mbit)。为了避免使用大容量的存储器。可采用了一种基于CORDIC( Coordinate Rotation Digital Computer)算法来产生正/余弦样本。该算法有线性的收敛域和序列特性。只要迭代次数足够,即可保证结果有足够的精度。并且用于混频的乘法器也可以省掉。从而还节省了大量的逻辑硬件资源。使得数字下变频更易于用FPGA来实现。
为DDC输入信号的采样频率。正弦波样木可以用实时计算的方法产生,但这只适用信号采样频率很低的情况。在软件无线电高速信号采样频率的情况下,NCO实时计算的方法是不可取的。NCO产生正弦波样本通常采用查表法,通过输入的相位数据来寻址查表输出相应的正弦波幅值。对于一个相位位数为n,输出信号幅度位数为M的数控振荡器,这就需要耗费大量的ROM资源(2nX Mbit)。为了避免使用大容量的存储器。可采用了一种基于CORDIC( Coordinate Rotation Digital Computer)算法来产生正/余弦样本。该算法有线性的收敛域和序列特性。只要迭代次数足够,即可保证结果有足够的精度。并且用于混频的乘法器也可以省掉。从而还节省了大量的逻辑硬件资源。使得数字下变频更易于用FPGA来实现。3.1 CORDIC算法
CORDIC算法基本原理是:设初始向量x0+jy0经旋转 角度后得到的向量 xn+jyn即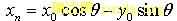 ,
, 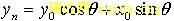 ,设旋转基本角度 θi,令
,设旋转基本角度 θi,令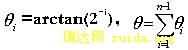 ,那么初始向量可通过一系列的基本角度 θi的旋转,逐渐逼近目标向量。在旋转模式下,如果设Z0=θ ,根据J,S,WALTER的推导有:
,那么初始向量可通过一系列的基本角度 θi的旋转,逐渐逼近目标向量。在旋转模式下,如果设Z0=θ ,根据J,S,WALTER的推导有:
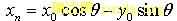 ,
, 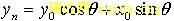 ,设旋转基本角度 θi,令
,设旋转基本角度 θi,令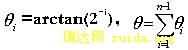 ,那么初始向量可通过一系列的基本角度 θi的旋转,逐渐逼近目标向量。在旋转模式下,如果设Z0=θ ,根据J,S,WALTER的推导有:
,那么初始向量可通过一系列的基本角度 θi的旋转,逐渐逼近目标向量。在旋转模式下,如果设Z0=θ ,根据J,S,WALTER的推导有: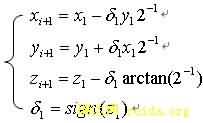 (1) (1) |
其中
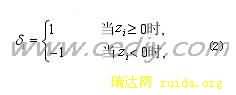
δi代表向量旋转方向
经过n 次旋转迭代后的结果为:
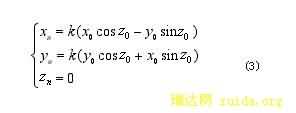
其中,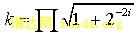 ,称为模校正因子。如果令
,称为模校正因子。如果令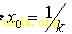 , y0=0,则
, y0=0,则  ,由上述推导可知:若已知角度Z0 和初始向量的 x0,y0 可由式(1)迭代运算得到角度 Z0的正余弦值,而式(3)中的迭代运算用硬件实现时非常方便,只有加(减)和移位操作。
,由上述推导可知:若已知角度Z0 和初始向量的 x0,y0 可由式(1)迭代运算得到角度 Z0的正余弦值,而式(3)中的迭代运算用硬件实现时非常方便,只有加(减)和移位操作。
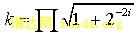 ,称为模校正因子。如果令
,称为模校正因子。如果令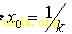 , y0=0,则
, y0=0,则  ,由上述推导可知:若已知角度Z0 和初始向量的 x0,y0 可由式(1)迭代运算得到角度 Z0的正余弦值,而式(3)中的迭代运算用硬件实现时非常方便,只有加(减)和移位操作。
,由上述推导可知:若已知角度Z0 和初始向量的 x0,y0 可由式(1)迭代运算得到角度 Z0的正余弦值,而式(3)中的迭代运算用硬件实现时非常方便,只有加(减)和移位操作。3.2 基于CORDIC算法实现NCO
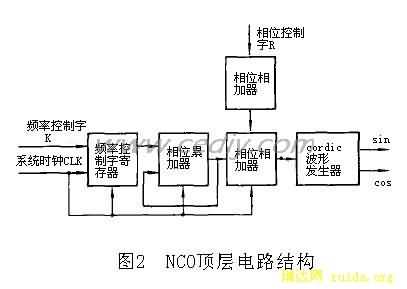
我们设计的NCO顶层结构为图2所示。我们可以看到,频率控制字寄存器将接收到的频率控制字K送入相位累加器,累加器对系统时钟进行累加计数,当到达输入频率控制字的值时对相位进行累加,随后将累加值送入相位相加器,与相位控制字寄存器接收到的初始相位相加,得到当前的相位值。经过上述相位处理之后,即可获得相位的正/余弦相位序列,将此序列送入基于CORDIC算法的波形发生器,最终获得两路正交的正/余弦输出序列。
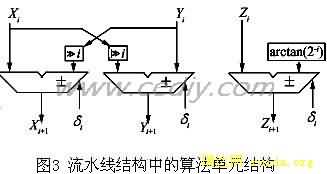
采用了流水线型实现结构,它用n级相似的算法单元在同一个时钟周期内并行工作,每级算法单元的具体实现结构如图3所示。图中的三个累加器分别完成了该级中xi,yi,zi的迭代,累加器的加/减控制信号为上一级算法单元中的di信号,两个i位的右移寄存器(注:图中的>>i表示右移i位)完成了迭代等式中的乘2-i运算,而该级的基本旋转角度值(2-i)可以采用直接硬连接。
流水线结构的最大优点在于它的运算速度很快在任何一个时钟周期,n级算法单元都同时工作,如在输入端连续不断地送入数据,那么在n个时钟周期的延迟之后,输出端将连续得到相应的下变频后的数据与传统的串行结构相比,流水线结构的运算速提高了n倍。图4给出了16级流水线算法
的实现结构虚线框中部分是个初始化旋转单元,是因为  。由此可见,当迭代的次数n趋近于无穷大时,所被 覆盖的角度只能是在-99.9度~99.9度之间,若想让 的覆盖范围扩展到
。由此可见,当迭代的次数n趋近于无穷大时,所被 覆盖的角度只能是在-99.9度~99.9度之间,若想让 的覆盖范围扩展到 ,必须在迭代之前再增加一个初始化旋转,将输入向量先旋转
,必须在迭代之前再增加一个初始化旋转,将输入向量先旋转 ,之后是16级流水线算法单元,最右边的是级的基本旋转角度值(2-i),di为各级累加器加/减控制信号"X0,Y0,Z0为下变频模块的数据输端口,Xn,Yn,Zn是三个输出端口"。
,之后是16级流水线算法单元,最右边的是级的基本旋转角度值(2-i),di为各级累加器加/减控制信号"X0,Y0,Z0为下变频模块的数据输端口,Xn,Yn,Zn是三个输出端口"。
 。由此可见,当迭代的次数n趋近于无穷大时,所被 覆盖的角度只能是在-99.9度~99.9度之间,若想让 的覆盖范围扩展到
。由此可见,当迭代的次数n趋近于无穷大时,所被 覆盖的角度只能是在-99.9度~99.9度之间,若想让 的覆盖范围扩展到 ,必须在迭代之前再增加一个初始化旋转,将输入向量先旋转
,必须在迭代之前再增加一个初始化旋转,将输入向量先旋转 ,之后是16级流水线算法单元,最右边的是级的基本旋转角度值(2-i),di为各级累加器加/减控制信号"X0,Y0,Z0为下变频模块的数据输端口,Xn,Yn,Zn是三个输出端口"。
,之后是16级流水线算法单元,最右边的是级的基本旋转角度值(2-i),di为各级累加器加/减控制信号"X0,Y0,Z0为下变频模块的数据输端口,Xn,Yn,Zn是三个输出端口"。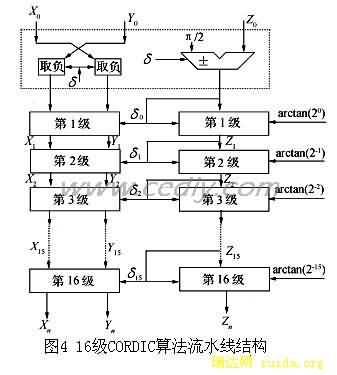
3.3 初始化旋转单元代码
输入为x_in y_in z_in 输出为 phi,eps,r 定义信号为x,y,z
---Test for x_in<0 rotate 0,+90,or -90 degrees
IF x_in>o THEN
x <=x_in;
y<=y_in;
z<=z_in;
ELSEIF y_in>0 THEN
x<=y_in;
y<=-x_in;
z<=z_in+90;
ELSE
x<=-y_in;
y<=x_in;
z<=z_in-90;
END IF;
4 积分梳状(CIC)滤波器的FPGA设计
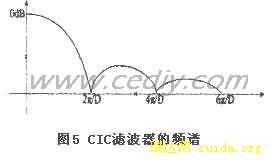
CIC滤波器由两部分组成,积分器和梳状滤波器的级联其冲击响应为
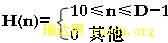 (4)
(4)
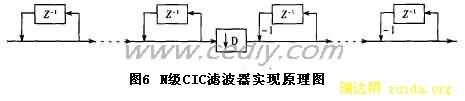
图5显示的是它的频谱图。CIC所有系数都为1,实现起来极其简单,它不需要任何乘法运算,不需要存储滤波器系数。为了加大阻带衰减,通常采用N级CIC滤波器如图6所示。
5 半带抽取滤波器(HBF)的FPGA设计
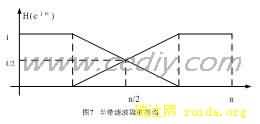
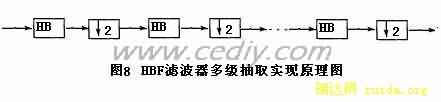
HBF滤波器特别适合于实现2的幂次方倍的抽取,且计算效率高、实时性强。其频谱如图7所示。半带滤波器是频率响应满足阻带宽度与通带宽度相等,当抽取率为2的幂次方时实现如图8所示。
6 使用Dspbuilder低通滤波器的设计
使用Dspbuilder可以方便地在图形化环境中设计FIR数字滤波器,而且系数的计算可以借助MATLAB强大的计算能力和现成的滤波器设计工具来完成。
6.1 利用MATLAB确定滤波器的参数
低通滤波器采用FIR滤波器。FIR滤波器由于有线性相位稳定性好等特征被广泛运用。并且其结构易于用FPGA实现 MATLAB中FDA TOOL的Filter Design & Analysis Tool对滤波器的设计很有用。进入滤波器设计界面,选择类型LOWPASS,设计方法为WINDOW,除数为15,窗口类型为Kaiser,Beta为0.5 另 为48KHZ, 为10.8KHZ。此时利用FDA TOOL有关工具分析反应设计的滤波器的各种特性如幅频,相频,冲激,阶跃响应零极点等。导出滤波器系数,然后对系数进行量化为位宽为9位绝对值为8位的数值.导出后分另扩大2^8倍得到整数:-19 6 29 3 -45 -25 92 212 212 92 -25 -45 3 29 6 -19。
6.2 FIR滤波器的设计
FIR滤波器采用直接型结构,主要由移位寄存、乘法器和加法器组成。其设计思想是利用 DSPBuilder模块直接实现乘法器和加法器。基于乘、加的设计比较简单,系统工作速度较高,但占用的资源很大,因速度要求较高、阶数较小的滤波器设计。利用DSPBuilder模块设计的FIR滤波器很容易进行能扩展,输入数据的位宽可以根据实际的需要进行调整。如图9为四阶FIR的subsystem 要实现16阶或更高阶的滤波器,只需要将滤波器级联数据相加即可。

7 仿真验证
Altera 的DPSBuilder提供的HIL模块能很好的完成硬件仿真,HIL可以在Simulink模型与FPGA开发板间通过JTAG通信接口建立一种联系,从而实现基于MATLAB/DSPBuilder平台的硬件仿真。本文选用Altera公司的Cyclone系列EP1C6Q240C8为主芯片的开发板进行仿真。NCO的仿真结果如图10所示。
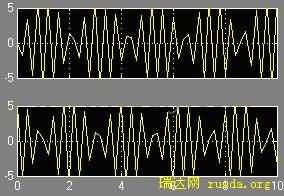
图10 两输出I/Q瞬时仿真结果
由仿真结果可见用CORDIC算法设计出来的NCO还是比较理想的,进一步说明模型与代码的正确性。
8 结语
基于CORDIC上算法设计的下变频器,不仅完全满足通常各类接收机的要求,而且还能克服传统NCO设计方法所要消耗的大量ROM。FPGA固有的硬件可重构特点适合于下变频器的开发和设计也适合于软件无线电的开放平台,本文中采用DSPBuilder系统工具和硬件传真模块极大的缩短了开发和仿真的时间,也方便了系统的更改和扩展。可使设计更加灵活,便捷。
参考文献
[1] 杨小牛,楼才义,徐建良.软件无线电原理与应用.北京:电子工业出版社,2001年
[2] 潘 松,黄继业,王国栋.现代DSP技术.西安:西安电子科技大学出版社,2003年
[3] 郑瑾,葛临东.基于流水线CORDIC算法的数字下变频实现. 数字与数据处理,2006年第10期
[4] 潘松,黄继业. EDA技术与VHDL(第二版),清华大学出版社,2007年
[5] Uwe Meyer-base 著书,刘凌译. 数字信号处理的FPGA实现(第二版),清华大学出版社2006年
[6] EDA先锋工作室. Altera FPGA/CPLD 设计(基础篇),人民邮电出版社2005年
 打印本文
打印本文  关闭窗口
关闭窗口