2PSK/BPSK调制部分框图

1、M序列发生器
         实际的数字基带信号是随机的，为了实验和测试方便，一般都是用M序列发生器产生一个伪随机序列来充当数字基带信号源。按照本原多项式f(x)=X5+X3+1组成的五级线性移位寄存器，就可得到31位码长的M序列。
         码元定时与载波的关系可以是同步的，以便清晰观察码元变化时对应调制载波的相应变化；也可以是异步的，因为实际的系统都是异步的，码元速率约为1Mbt/s。

2、相对移相和绝对移相

移相键控分为绝对移相和相对移相两种。以未调载波的相位作为基准的相位调制叫作绝对移相。以二进制调相为例，取码元为“1”时，调制后载波与未调载波同相；取码元为“0”时，调制后载波与未调载波反相；“1”和“0”时调制后载波相位差1800。绝对移相的波形如下图所示。

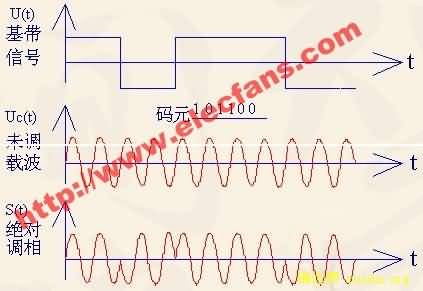
绝对移相的波形示意图

在同步解调的PSK系统中，由于收端载波恢复存在相位含糊的问题，即恢复的载波可能与未调载波同相，也可能反相，以至使解调后的信码出现“0”、“1”倒置，发送为“1”码，解调后得到“0”码；发送为“0”码，解调后得到“1”码。这是我们所不希望的，为了克服这种现象，人们提出了相对移相方式。
          相对移相的调制规律是：每一个码元的载波相位不是以固定的未调载波相位作基准的，而是以相邻的前一个码元的载波相位来确定其相位的取值。例如，当某一码元取“1”时，它的载波相位与前一码元的载波同相；码元取“0”时，它的载波相位与前一码元的载波反相。相对移相的波形如下图所示。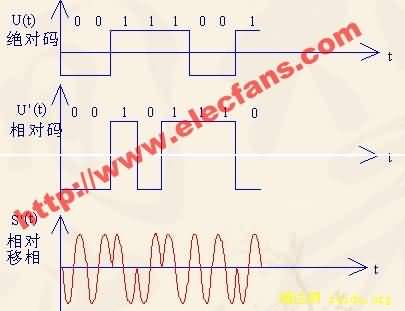

图4-4 相对移相的波形示意图
一般情况下，相对移相可通过对信码进行变换和绝对移相来实现。将信码经过差分编码变换成新的码组——相对码，再利用相对码对载波进行绝对移相，使输出的已调载波相位满足相对移相的相位关系。

设绝对码为{ai}，相对码为{bi}，则二相编码的逻辑关系为：     bi = ai–bi-1           (1)
   差分编码的功能可由一个模二和电路和一级移位寄存器组成。
    对应于差分编码，在解调部分有——差分译码。差分译码的逻辑为：
                        ci =bi +bi-1                     (2)
    将(1)式代入(2)式，得
                       Ci=ai-bi-1+bi-1
                  ∵    bi-1-bi-1=0       ∴    Ci=ai+0=ai
    这样，经差分译码后就恢复了原始的信码序列。
    差分译码的功能同样可由一个模二和电路和一级移位寄存器组成。

图4－5绝对码实现相对移相的过程

3、 调相电路
调相电路可由模拟相乘器实现，也可由数字电路实现。实验中的调相电路是由数字选择器(74LS153)完成。当2脚和14脚同时为高电平时，7脚输出与3脚输入的0相载波相同；当2脚和14脚同时为低电平时，7脚输出与6脚输入的π相载波相同。这样就完成了差分信码对载波的相位调制。图4-5示出了一个数字序列的相对移相的过程。
 
数字调相器的主要指标
    在设计与调整一个数字调相器时，主要考虑的性能指标是调相误差和寄生调幅。
    (1) 调相误差
    由于电路不理想，往往引进附加的相移，使调相器输出信号的载波相位取值为0°及180°＋ΔΦ，我们把这个偏离的相角ΔΦ称为调相误差。调相器的调相误差相当于损失了有用信号的能量。
(2) 寄生调幅
    理想的二相相位调制器，当数码取“0”或“1”时，其输出信号的幅度应保持不变，即只有相位调制而没有附加幅度调制。但由于调制器的特性不均匀及脉冲高低电平的影响，使得“0”码和“1”码的输出信号幅度不等。设“0”码和“1”码所对应的输出信号幅度分别为Uom或Uim，则寄生调幅为：
              m=(Uom-Uim)/(Uom+Uim)×100%                    (3)
解调
2PSK系统的解调部分框图如下图所示

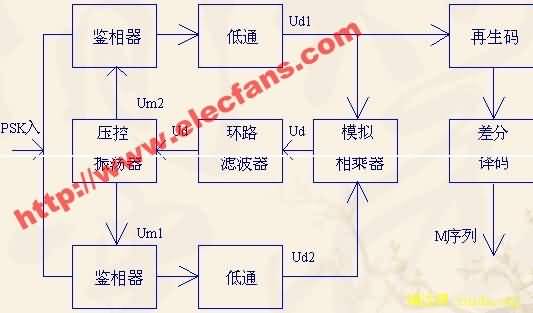
   1、  本实验采用同相正交环，同相正交环又叫科斯塔斯（Cosatas）环。原理框图如下图所示。

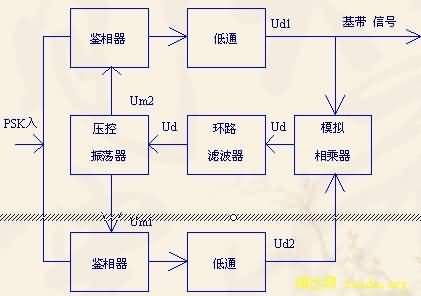
图4－7  同相正交环原理框图

2、集成电路压控振荡器（IC－VCO）
    压控振荡器（VCO）是锁相环的关键部件，它的频率调节和压控灵敏度决定于锁相环的跟踪性能。
    实验电路采用一种集成电路的压控振荡器74S124。集成片配以简单的外部元件并加以适当调整，即可得到令人满意的结果。如图所示。

集成片的每一个振荡器都有两个电压控制端，Vr用于控制频率范围（14脚），Vf用于控制频率范围调节（1脚）。外接电容器Cext用于选择振荡器的中心频率。当Vr和Vf取值适当，振荡器工作正常时，振荡器频率f0与Cext的关系近似为：
  f0=5×10－4/Cext      （4）
f0与Cext的关系曲线如图所示。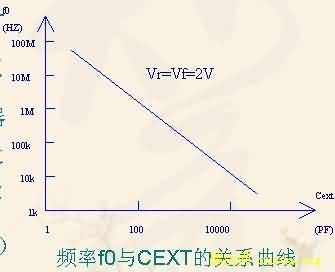

由右图的曲线可以看出，随Vr的增大，VCO的压控灵敏度和线性范围都在增大。选取适当的Vr值和Cext值，将误差电压经线性变换后充当控制电压Vf，这样就可实现由误差电压控制VCO。当f0=10MHz时，一组典型的实验数据为Cext=27.5pf，Vr=3.76V，这时Vf在2.8V左右移动。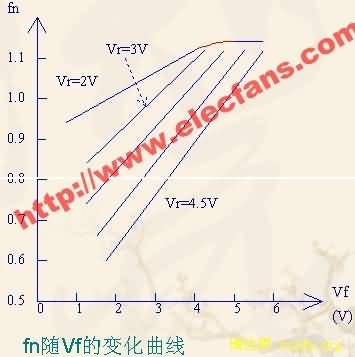

3、传输畸变和眼图
    数字信号经过非理想的传输系统必定产生畸变，为了衡量这种畸变的严重程度，一般都采用观察眼图的方式。眼图是示波器重复扫描所显示的波形，示波器的输入信号是解调后经低通滤波器恢复的未经再生的基带信号，同步信号是位定时。这种波形示意图如下图所示。

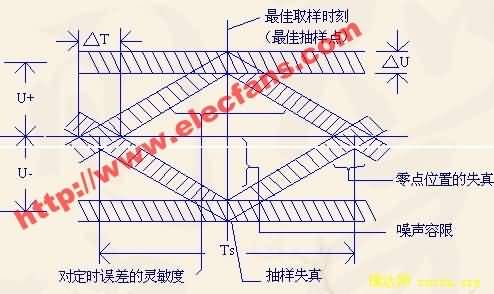
图4-8  眼图

衡量眼图的几个重要参数有：
眼图开启度（U-2ΔU）/U  (U = U+ + U-)
   指在最佳抽样点处眼图幅度的“张开”程度。无畸变眼图的开启度为100%。
（2）“眼皮”厚度2ΔU/U
   指在最佳抽样点处眼图幅度的闭合部分与最大幅度之比，无畸变眼图的“眼皮”后度为0。
（3）交叉点发散度ΔT/TS
   指眼图波形过零点交叉线的发散程度。无畸变眼图的交叉发散度为0。
（4）正、负极性不对称度|（U+ - U-）|/|（U+ + U-）|
   指在最佳抽样点处眼图正、负幅度不对称的程度。无畸变眼图的极性不对称度为0。
如果传输信道不理想，产生传输畸变，就会很敏感地由眼图的这几个参数反映出来。其后果可以看成有效信号的能量损失。可以推导出，等效信号信噪比的损失量ΔEb/No与眼图开启度（U-2ΔU）/U有如下关系：
 ΔEb/No=20log[（U-2ΔU）/U]     (dB)       (5)
同样，交叉点发散度对信噪比损失的影响也可以等效为眼图开启度对信噪比损失的影响，这里不再详述。
转载请说明来至 http://www.elecfans.com