图9-5-1(a)所示是一个RLC串联电路，初始条件是、，利用上一节的电路元件及其模型，可画出相应的复频域电路模型，即运算电路，如图9-5-1(b)所示。

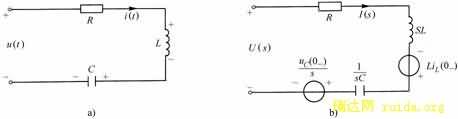
图9-5-1

根据复频域的KVL，得到：

令，则上式写为：

式中称为RLC串联电路的运算阻抗，其例数称为运算导纳。正弦稳态电路中RLC串联阻抗是，形式上与相似。

应用拉普拉斯变换分析线性动态电路过渡过程的方法，通常被称为运算法。

下面请看几个例题。

例9-5-1 图9-5-2(a)所示电路，开关闭合前处于零状态，试求电路。

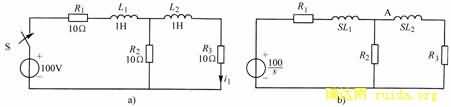
图9-5-2例9-5-1附图

解：因为电路原处于零状态，画出其运算电路的如图9-5-2(b)所示，采用戴维南定理，求AB以左电路的戴维南等效电压：

等效运算阻抗：

故电流的象函数：

最后求原函数：

例9-5-2 如图9-5-3（a）所示，

开关K在位置1时电路处于稳态，在时将开关置于位置2，求。

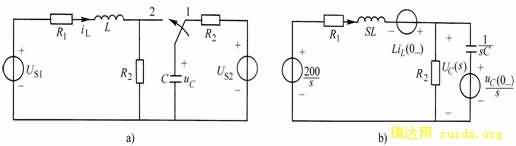
如9-5-3例9-5-2附图

解：当t＜0时，开关位于“1”且电路处于稳态，则：

，

作运算电路如图9-5-3（b）所示，由节点电压法：

将作部分分式展开并求出相应系数得：

最后得原函数：

例9-5-3 并联电路如图9-5-4（a）所示，换路前电路处于零状态，电流源为单位冲激函数，试求和。

图9-5-4例9-5-3附图

解：作运算电路如图9-5-4（b）所示：

原函数：

，

原函数：