摘  要：研究了变压器绕组的机电耦合振动稳定性问题，建立了变压器绕组轴向机电耦合的动力学模型。将变压器绕组的漏磁场简化成二维磁场，得到其解析解，采用机电耦合系统的Lagrange方程，分析得到变压器绕组机电耦合的非线性振动方程，以及简化的耦合振动方程。应用动力学理论分析载流的变压器绕组轴向振动的稳定性，得到了模型变压器绕组主要设计参数的稳定域和不稳定域，分析大电流引起变压器绕组失稳的机理。
    关键词：电力变压器；机电耦合振动；稳定性; 绕组变形

1  Introduction

   A power transformer has to be designed and built to withstand thermal and mechanical stresses resultingfrom all external short circuits during its normal life, which may be expected to exceed 20 years. An extensive program of transformer short circuit testing and analysis has been carried out to define failure modes and determine the limits of design parameters ^[1,2]. The windings of transformer may be destroyed by various causes, such as collapse of the conductors, failure in the insulation and erosion of the conductor insulation caused by rubbing, which lead to electrical breakdown. So it is essential for the designer to estimate the stability, displacements and forces of the windings during short circuit conditions.
   In conventional analysis, the winding of power transformer is regarded as a mass-spring system. The mass of the system is made of coils and insulators of the windings, and the spring of the system is come from the elastic deformation of the insulators of the windings. The electromagnetic forces are regarded as varying with current through the windings. However, in the process of winding axial vibration, it has been observed that the electromagnetic forces varied with displacements of windings ^[1~3].
    In this paper, a new dynamic model for axial vibration of transformer winding is established. In the new model, magnetic forces vary with the displacements of windings. The stable conditions are obtained for the design of new structure of transformer windings.
2  Leakage Magnetic Field of Transformer
    The calculation model is a 50Hz power transformer with 2-windings. It is specially designed for research purpose. Fig. 1 shows the leakage magnetic field analysis model for this transformer.
    The currents through the windings are determined by the equations.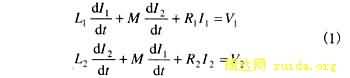

where,
    L_i  is the self inductance of i th winding.
    I_i   is the current through i th winding.
    V_i  is the voltage applied to i th winding.
      R_i  is the resistance of i th winding.
    M  is the mutual inductance between two windings.

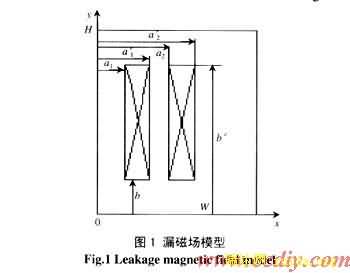
    The model-transformer leakage magnetic field is solved by a formulation in terms of magnetic vector potential A. The magnetic induction intensity B is given by Curl A. The govern equation of the transformer leakage magnetic field is as follows ^[4]:

 current density in the winding. u₁ and u₂ are axial displacements of windings.
    The solution of this transformer 2-dimensional leakage magnetic fields can be obtained by analytical method. The analytical solution is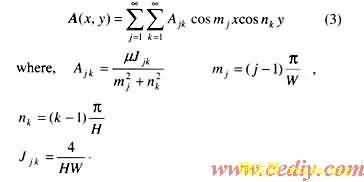

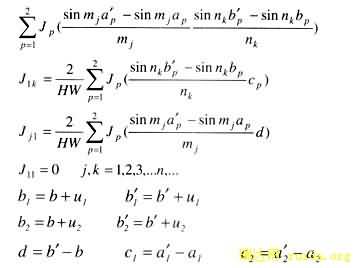
    It is shown from this solution that the magnetic vector potential A is a function of winding currents and displacements (u₁ and u₂).
3  Vibration Equations of Trans-former Winding
    In this paper, each winding of the transformer is regarded as a mass. Taking each winding with its elastic supports as a spring-mass vibration system, we have a 2-freedom vibration system with nonlinear magnetic forces to the model transformer. The governing equations of this dynamic problem can be obtained by the Lagrange-Maxwell equation ^[5].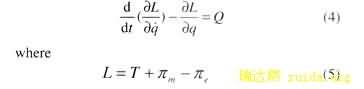

and Q is generalized force of the system, q is  generalized coordinate of the system. T, p_m and p_e are the kinetic energy, elastic energy and magnetic energy of the system, respectively. To the electromechanical coupled vibration of transformer  windings, we haveKinetic energy of the system:

where
    m_i  is mass of i th winding.
    k_i   is stiffness of elastic support of i th winding.
    f_i   is magnetic forces acting on the winding. The magnetic forces can be expressed as:

   It can be seen, from equation (10) and (11), that the relation between magnetic forces and the winding displacements (u₁ and u₂) is nonlinear. If the displacement of transformer winding is small enough, it is possible to approximate this nonlinear relation to a linear function. These linealy approximate magnetic forces are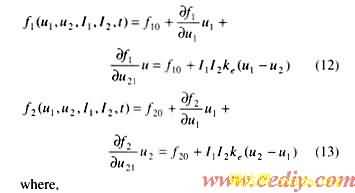

where,
f₁₀ and f₂₀ are magnetic forces on the outer and inner windings, when the displacements of winding are zero. k_e is magnetic stiffness of winding, which is defined by magnetic forces formulation (12) or (13), and related to the configuration of the transformer windings.
    For the model transformer’s windings, the magnetic forces are calculated by E_q(12) and (13). The various values of winding’s displacements are used to calculate the magnetic forces, and the typical results of the magnetic force are shown in Fig.2.

    At the static equilibrium point of the transformer’s windings, the magnetic forces f10 and f20 are equal to zero. For the model transformer, Fig. 2 shows that their values are almost equal to zero.
    Substituting equation (12) and (13) into equation (9), we get following coupled vibration equations for the transformer’s windings

    Equation (9), (1) and (2) are nonlinear electromechanical coupled vibration equations for the transformer windings. Equation (14), (1) and (2) are the simplified forms. In this paper, these simplified equations are used to assess vibration stability of the transformer’s windings.
4  Stability of The Transfor-mer’s Windings

    When the ampere-turn distributions in inner and outer windings are unbalanced (such as the unbalance caused by winding displacement along axial), the windings repulse each other. The axial magnetic force between inner and outer windings is a function of winding’s relative displacements d = u₁ - u_2. It can be obtained by an analytical solution (Eq.(10) and Eq.(11)). The currents through the winding are given by Eq.(1). The magnetic forces in axial direction are shown in Fig.2. It is shown that the magnetic forces increase with the increasing of winding’s relative distance d. When d/H<<1 (H is the height of transformer winding), the relationship between magnetic force and the winding’s relative displacement is nearly linear. We can get the magnetic stiffness k_e of the transformer’s windings from Fig.2.
  Based on the stability of dynamic system, we study the stability of the coupled vibration of the transformer’s windings with AC currents through the transformer’s windings. In equation (14), lets
 

Where, w is angular frequency of electric current. Substituting equation (15) into coupled vibration equations (14), the coupled vibration equations become

    They are Mathieu’s differential equation group without damping. Because of the complexity of Eq.(16), there is no analytical solution obtained. As a general transformer windings' vibration problem, it is indispensable to solve Eq.(16) by numerical method. To the model transformer, we have
     m₁=m₂=m    k₁=k₂=2       (17)

Lets d=u₁-u₂  , it’s the relative displacement of two windings. Considering of Eq.(17), the following vibration equation is obtained from equations (16).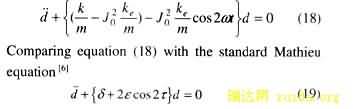

   The well known solution of the Mathieu equation (e.g. reference [6]) is presented here in the form of Strutt diagram in figure 3. The stability and instability regions are shown in the Strutt diagram. For the vibration system with damping, the stable region expands ^[6].

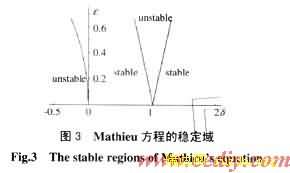
   Examining the definitions of d and e in equation (20), one can see that l and I₀ are important parameters influencing d and e. The parameter I₀ appears in the expressions for both d and e. With the increasing of I₀ , e  increases and d decreases. Thus, it can be concluded that the possibility of instability is greater at high current I₀. This means that the high currents through the transformer windings may cause instability of the winding’s vibration. Parameter l influences d only, and the increase of l leads to increase of d, but without any changes in e. Therefore, increasing l may be useful to stabilize axial vibration of transformer windings. This means that increasing the stiffness of the supporting structure of the windings is useful to the stability of the axial vibration of transformer windings. The constant l_e is another parameter which alters the magnitude of d and e , as discussed previously, which fully depends on the configuration of the transformer windings.
5  Conclusion
    This paper deals with the axial vibration problem of transformer winding by electromechanical coupled theory. The following research is included.
   （1）The model transformer leakage field is simplified to a 2-dimensional magnetic field. The analytical formulation of the transformer leakage field is obtained.
   （2）Based on the electromechanical coupling theory, the axial vibration equations of transformer windings are obtained. Assuming the electromagnetic forces vary linearly with the winding displacements, the simplified electromechanical coupled vibration equations of the transformer windings are presented.
   （3） According to the stability theory of dynamic system, stability conditions for axial vibrations of transformer windings are obtained. It can be used to guide the design of new transformer windings.
   （4）It is shown that increase in the stiffness of transformer winding supporting structure is benefical to the stability of axial vibration of transformer windings.

Reference

[1]  Wang Z Q, Shi C L, Peng Z Z. The axial dynamic response of large power transformer windings under short circuit conditions by FEM [C]. New Advances in Model Syntheses of Large Structure. Edited by L.Jezequel, 1997.
[2]  Quinney D.A. et al. Dynamic response of a power-transformer winding under axial short-circuit conditions [J]. IEE Proc. 1981,1128(2)：114-118.
[3]  Yasuro Hori, Kenchi Okuyama. Axial vibration analysis of transformer windings under short circuit conditions[J]. IEEE Trans. on Power Apparatus and System, 1980, PAS-99(2)：443-451.
[4]  汤缊璆(Tang Y.Q.) 电机磁场（Magnetic field in electric machine）[M]. 北京：科学出版社（Beijing: Science press）,1982. 
[5]  Chattopadhyay S. Magnetoelastic instability of structures carrying electric current [J]. Int. J. Solids structures,1997, 15(3)：467-477.
[6]  Nayfeh A.H, Mook D T. Nonlinear oscillations[M]. England: John Wily,1979 .