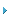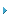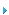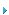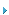一种新型的调光电子镇流器_瑞达电器资料网,华玉生活

摘要：介绍了一种新型的荧光灯调光控制方式，即通过不对称占空比调制的方式控制荧光灯的输出功率。首先，基于功率关系的荧光灯模型，通过基波近似的方法得到了控制方程，得出了荧光灯的调光特性。然后，应用一个半桥式串联谐振并联负载电路为例，给出了设计步骤，仿真及实验结果。

关键词：调光电子镇流器；占空比调制；谐振；功率模型

1 引言

高频调光电子镇流器以其效率高，无频闪，体积小等优点，获得了技术界的广泛认同。一般来说，可以通过调节电子镇流器电路的3个参数（直流母线电压，占空比和开关频率）实现调光。

通常，调节直流母线电压可以较好地实现调光的目的，但是，由于电子镇流器都有功率因数要求，如果采用普通的Boost电路作为功率因数校正，直流母线电压至少是输入电压的两倍，这样调光就被限制在了一个很小的范围，而且这种方法的控制电路比较复杂。调频调光是比较常用且简单的方法，但是，开关频率的不断变化，会使电路产生严重的电磁干扰，使EMC的设计比较困难，而且调频调光有一个固有的不稳定区，当频率达到某一值时荧光灯的输出功率会迅速变化，这会给实际应用带来麻烦。占空比的调节通常是指对称的占空比调节方式，这种方式虽然可以使调光特性曲线很平滑，但随着占空比的减小，波形的畸变程度大大加重，会影响荧光灯的寿命。

为了克服上述几种调光方法的缺点，使之能达到平滑地调光，且不产生很大的电磁干扰，本文提出了一种新型的调光方法，即不对称占空比的调光方法，可以达到理想的效果。

2 基本电路

图1为电子镇流器最基本的半桥谐振电路，输入电压V_in由市电经过整流桥直接得到，通过控制开关管S₁和S₂给谐振电路提供电流；C_s为隔直电容，使A和B两端得到一个对称方波电压信号，为使它基本上不参与谐振，因此，要求C_s》C_f，一般取C_s>10C_f就可满足条件；L_s和C_f分别是谐振电感、电容，为荧光灯提供必要的启动电压，并保证荧光灯正常工作时能稳定运行。

图1 基本电路

在图1的基本电路中，通过调节S₁及S₂的占空比（任何时候开关S₁及S₂导通时间互补），改变A和B两端的输入基波电压的幅值，便可以改变荧光灯的输入功率，从而达到调光的目的。

荧光灯是一种非线性负载，因此，需要建立一个适当的电路模型以便分析它的调光特性。本文通过对Philips T8－36W荧光灯（额定电压95V；额定电流0.31A）的测量，可以发现荧光灯的电压随功率的减小而线性增长，电流随功率的增长呈近似二次曲线的形式增长，因此，采用功率模型（以功率为自变量，电流和电压分别是功率的函数）对荧光灯的调光过程进行分析，可以得到与实际比较接近的结果。这里采用的模型如下：

V(P)=151－2P（1）

I(P)=2.28×10^－3＋5.8×10^－3P＋1.62×10^－4P2 （2）

式中：P为荧光灯的功率。

由式（1）和式（2）可以得出灯的等效电阻与功率的关系：R(P)=V(P)/I(P)。其关系曲线如图2所示。

图2 荧光灯等效电阻与功率

3 调光分析

在图1所示的电路中，设计电路的谐振频率f₀=40kHz，输入电压V_in=300V，根据荧光灯额定电流及电压的关系，可以设计谐振参数：L_s=1.7mH，C_f=9.3nF。A和B之间的基波电压有效值为

v_AB1=V_insin(πD)（3）

式中：D是占空比，由于S₁及S₂占空比互补，且它们的调节对实际的效果是一样的，因此，规定本文中的D为S₁的占空比，而S₂的占空比为1－D。

根据电路基本原理，可以得出占空比与荧光灯的功率关系为

D(P)=（4）

式中：f_n为开关频率与电路谐振频率的比值；

Z为特征阻抗，Z=。

当f_n=1.05（额定工作点）时，可以得到占空比与功率的关系曲线如图3所示。

图3 开关占空比与功率的关系

从图3可以看到，调节占空比可以在整个功率范围内达到光滑的调光目的。但是在实际电路中，我们需要考虑开关的工作状态，当占空比过小时，开关的零电压工作条件就不能满足，这样会使开关体二极管出现反向恢复问题，导致开关损耗增加，电路的工作效率降低。为此，我们讨论开关工作在零电压状态的临界条件。

图4中v_ds1为S₁的漏—源极电压，v_AB1为谐振电路的基波电压，i_r为谐振电流，φ为两者的相位差。由图4可知，为达到软开关条件，必须满足式（5）

D>0.5－（5）

式中：φ与功率P有关，具体可由图1电路的基本关系得出，即

φ(P)=arctan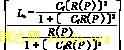（6）

图4 不对称占空比谐振电路基波电压及电流

它们的关系曲线如图5所示。从图5可以看到随着P的减小而减小，由式（5）可知对D的要求随P的减小而增大，对照图3与图5可以看到，当功率调到12W左右的时候，D降到0.11，而由图5及式（5）可以看到，当功率为12W时，要求D≥0.11。因此，通过不对称占空比的调节可以使荧光灯功率调到12W，事实上，这一数值对实际应用已经足够，因为，在更低的功率下，荧光灯的光输出会减小，即每瓦的流明数会减小，如果再减小功率将得不偿失。