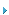摘    要：本文提出一种新的级联型多电平逆变器拓扑结构，通过负载将两个电压型三相逆变器级联在一起，该逆变器能作为一个三电平或四电平逆变器运行。本文对这种逆变器的基本结构和控制原理进行了分析。

　　关键词：级联型多电平逆变器；空间矢量

　　引言

　　在已经提出的多种多电平逆变器的拓扑结构中，最为典型的有：二极管钳位型、飞跨电容型、级联型。其中级联型逆变器具有不需要前两种电路所需的大量钳位二极管和钳位电容，结构简单、易于模块化、不存在电容电压不平衡问题且易于采用软开关技术，已被广泛地应用于灵活的电力系统和用户电力技术等领域。

　　为了增加输出电压的电平和提高波形质量，多种改进的级联型拓扑不断被研究者们提出来。在高压大功率应用领域，可以将级联型多电平逆变器的全桥逆变单元(FBC)用二极管钳位或电容钳位多电平逆变器代替，以减少所需的独立直流电源数。这种结构被称为混合电平混合型多电平逆变电路。在前面所叙的级联型多电平逆变器中，每个FBC的直流电源电压都相等。而且可以对各个FBC施以不同的电压，这种电路被称为非对称混合型多电平逆变电路。非对称混合型多电平逆变电路还有另外一种形式，即令每个FBC的电源电压相同，但每个FBC的主开关器件可以不同，这样每个FBC的工作频率可以不同。

　　不难发现，以上所有的级联型拓扑结构都有个共同特点：即都是对单相逆变电路进行级联，当采用这样的拓扑构成三相系统时，需要大量的直流电源。本文提出的一种基于三相级联的多电平逆变器，能输出与三电平逆变器或四电平逆变器相同的电压，而且不必每相都需要独立的直流电源。

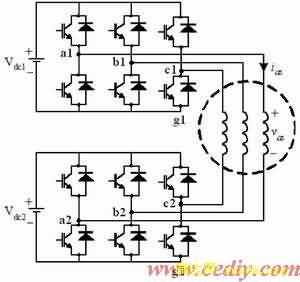
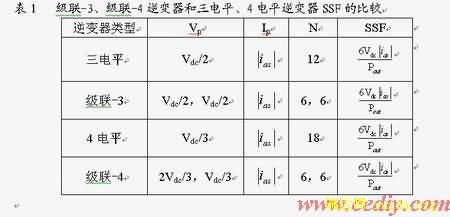
图1  基于三相级联的多电平逆变器

图2  级联型逆变器输出空间电压矢量图

图3  Vdc1=Vdc2输出电压、电流波形

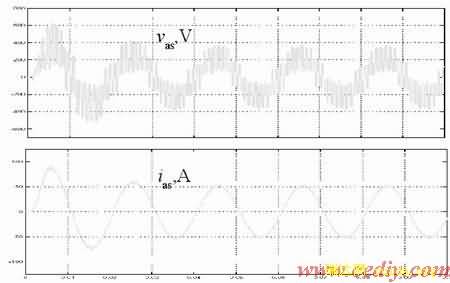
图4  Vdc1=2Vdc2输出电压、电流波形

　　基于三相级联的多电平逆变器

　　图1为一个基于三相级联的逆变器拓扑结构，它通过负载将两个三相电压型逆变器级联在一起。由于每个桥臂有两种开关状态，因此该逆变器共有64种开关状态。图2是该逆变器在不同直流电压比下的输出空间电压矢量图。从图2可以看出，通过设置不同的上下逆变器的直流电压比，该级联型逆变器可以作为一个二电平、三电平或四电平逆变器运行，分别称为级联-2、级联-3或级联-4逆变器。

　　有文献研究表明，当Vdc1=Vdc2=Vdc/2时，该逆变器的输出电压和一个三电平逆变器的输出电压完全相同；当Vdc1=2Vdc/3，Vdc2=Vdc/3时，该逆变器的输出电压和一个四电平逆变器的输出电压完全相同，其中Vdc为三电平逆变器或四电平逆变器直流侧的电源电压。

　　另外，对于一定功率等级的逆变器来说，其装置成本与开关应力系数(SSF—Switching Stress Factor)成正比，SSF定义如下：

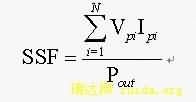
其中：N — 逆变器的功率开关器件个数
Vpi— 第i个器件关断时所承受的电压峰值
Ipi — 第i个器件导通时所通过的电流峰值
Pout— 逆变器的输出功率

　　表1给出了具有相同功率等级的级联-3、级联-4逆变器和三电平、四电平逆变器SSF的比较。表中级联型逆变器的Vp和N有两个值，分别对应于上下不同的级联单元。

　　从表1中可以看出：

1. 四种逆变器的SSF完全相等，故其装置成本基本相同；
2. 四电平逆变器所需的器件最多，故其开关损耗最大；
3. 级联-4逆变器上侧逆变单元的器件的额定电压最高。

　　基于三相级联的多电平逆变器的调制

　　针对该级联型逆变器结构上的特点，可以对上下两个逆变器进行联合调制或分别进行单独调制。联合调制是将上下两个逆变器视为一个整体，然后运用多电平逆变器的调制方法进行调制，最常用的是空间矢量调制(SVM)技术。例如，对于级联-3逆变器来说，它有64个不同的开关状态，能产生19个不同的空间电压矢量。单独调制是指分别对上下两个逆变器采取不同的调制策略。例如，对上侧逆变器可实施低频PWM调制，以提供负载所需的绝大部分功率，对下侧逆变器可实施高频PWM调制，以改善负载上的电压电流波形。

　　仿真验证

　　采用Matlab的Simulink作为仿真工具，并采用联合SPWM调制方法对图1中的电路进行了仿真。载波比为18，每相负载由100W的电阻、50.1H的电感串联构成。其中直流电压比取1:1时的输出电压电流波形如图3所示。图4为直流电压比取2:1时的输出电压电流波形。

　　结语

　　本文提出的基于三相级联的多电平逆变器拓扑，通过负载将两个电压型三相逆变器级联在一起，相对于普通的三电平逆变器来说，该逆变器具有更多的冗余开关状态，这就为减少开关动作次数和减少谐波的优化控制提供了可能性；相对于普通的四电平逆变器来说，该逆变器只需较少的开关器件，从而简化了电路，降低了成本；相对于由传统的级联型逆变器构成的三相系统来说，该逆变器节省了大量的直流电源。另外，这种新型多电平逆变器的上侧和(或)下侧逆变器可直接使用商用成品，为整个系统的设计提供了方便。

参考文献

1 K.A. Corzine, S.D. Sudhoff, and C.A. Whitcomb. Performance characteristics of a cascaded two-level converter. IEEE trans. on Energy Conversion, 1999, 14(3): 433-439
2 Keith A. Corzine, Mike W. Wielebski, Peng Fangzheng and Jin Wang. Control of cascaded multilevel inverters. IEEE Trans. on Power Electronics, 2004, 19(3): 732-738