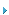摘 要:DC-DC变换器的数字控制相对于传统的模拟控制有很多优点。求解变换器的离散数学模型是设计其数字控制系统的基础。以boost变换器为例,应用线性平均法、准线性法和精确离散法分别求解DC-DC变换器的平均离散模型、准线性离散模型和精确离散模型;仿真分析三种离散模型在各种扰动下的响应。结果表明准线性模型能精确地描述系统在各种扰动情况下的响应,且可以方便地应用于变换器的数字控制的设计,以实现控制的自适应。
关键词:电力电子;DC-DC变换器;数字控制;建模
引言
DC-DC变换器的数字控制相对于传统的模拟控制不但具有可靠、稳定、设计灵活等优点,而且可实现复杂的非线性控制策略,以提高控制的动态和稳态性能。近年来随着各种性价比更高的微控制器(MCU)和数字信号处理器(DSP)的出现,使得DC-DC变换器数字控制的实现成为可能[1~3],其结构如图1所示。数字控制器的性能取决于控制策略和参数的选择,而变换器离散数学模型是控制策略和参数选择的基础,因此有必要分析比较各种建模方法的特点,选择合适的离散模型设计数字控制系统。本文给出了平均离散模型、准线性离散模型和精确离散模型三种建模方法,分析比较其各自的特点和应用。
1变换器三种离散模型
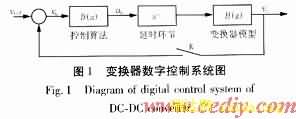
本文以boost变换器为例求解其平均离散模型、准线性离散模型和精确离散模型,该电路如图2所示。
在求解离散模型时做如下假设:
1) 变换器中的开关是理想的,即开关的开通和关断瞬间完成,不考虑损耗。
2) 除输出负载等效电阻外,变换器中其它元件的参数恒定不变,不随工作状态和温度的变化而变化。
3) 变换器工作在连续模式下,系统只在两个拓扑间转换。
1.1平均离散模型
DC-DC变换器由于开关的不断开通和断开,所以系统在两个线性系统之间不断地切换,是一个强非线性系统。平均离散模型是该非线性系统的线性离散模型,其求解步骤分为两步:① 分析开关开通和断开的状态方程,根据状态空间平均法[4]求解平均状态方程。② 将平均状态方程离散化得到离散平均状态方程。
设带寄生参数boost变换器的状态变量为电感电流il和电容电压vc。分析Boost电路工作过程可得当变换器工作在连续电流模式时的状态方程为:


u表示开关的状态,开关闭合时u=1,开关断开时u=0,E为输入电压,vo为输出电压。
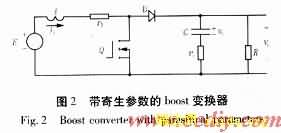
根据状态空间平均法,得变换器的平均状态方程为:
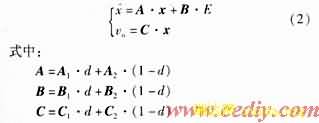
d为变换器在稳定工作点的占空比。
将上式离散化得离散小信号状态方程为:
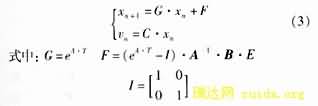
1.2准线性离散模型
DC-DC开关变换器是一个强非线性系统,平均离散模型只是在变换器额定工作点附近的近似线性化。为得到更精确模型,可采用分段线性化思想求解变换器的准线性模型。准线性模型由稳定点方程和该稳定点扰动方程两部分组成,稳定点方程描述系统稳定时的状态变量、占空比、输入电压和负载的关系;扰动方程描述系统在该稳定工作点的暂态特性。
1.2.1稳定点方程
分析boost变换器的工作过程,当闭环系统在输入电压和输出功率扰动后其状态变量满足如下等式:

将上式带入式(2)可得:
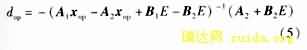
式中: xop为稳定点状态变量、dop为稳定时占空比,uref为输出参考电压。
1.2.2扰动方程
设变换器的状态变量、占空比可以表示为:
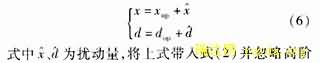
阶无穷小时可得:
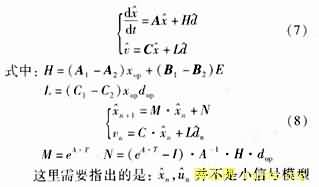
里的小信号,而是变换器工作时的瞬时值与系统稳定状态值之间的差值。离散方程的参数M,N,L随输入电压和负载的变化而变化。
1.3精确离散数学模型
因为DC-DC变换器的开关是不断开通和关断的,所以变换器本身就是一个离散的系统,因此可以直接分析变换器工作过程来建立精确的离散模型。Boost变换器在连续工作模式下有两个工作模态:模态1——开关Q导通,二极管D关断; 模态2——开关Q关断,二极管D导通。整个过程可以用图3表示。
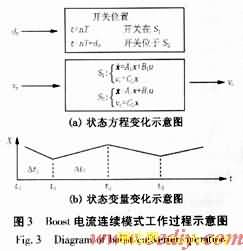
由图3可得:
![]()

比。这样就可以得到变换器在连续工作模式下精确离散模型为:
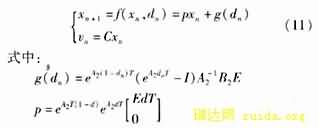
2模型比较
2.1仿真研究
为研究平均离散模型、准线性离散模型和精确离散模型的精确度的差别,本文仿真Boost电路三种模型在输入电压或输出负载变化时各模型输出电压的响应,并与Semtrix输出结果比较(Semtrix为开关电源仿真软件,其输出与实际电路输出很接近)。仿真电路的参数如表1所示。

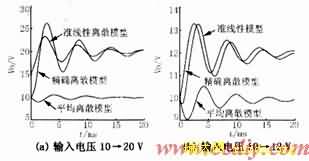
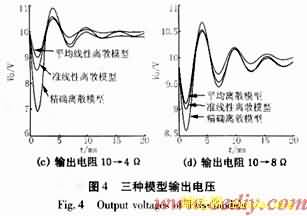
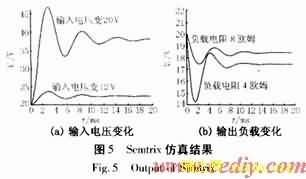
图4(a)、(b)是输入电压由10 V阶跃变化到20 V和12 V时三种模型的输出电压的响应图;图4(c)、(d)是输出负载由10 Ω变为4 Ω和8 Ω时三种模型输出电压响应图;图5是电路仿真软件Semtrix仿真的结果,通过比较可以得出:
1)三种离散模型都没反映变换器输出电压的高频分量。线性和准线性是基于状态空间平均法得到的,而状态空间平均法本身就忽略了高频分量的影响。精确离散模型因为采样频率为开关频率,所以也没有反映高频分量的影响。
2)在两种扰动情况下准线性模型的输出与精确离散模型和电路仿真软件Semtrix仿真输出结果相差很小,可以很精确描述系统的真实响应过程。平均离散模型在输入电压和输出功率变化很大时的输出响应较精确模型和Semtrix输出有较大的误差。
2.2应用分析
三种模型都有其各自的特点。平均离散模型求解简单,但其建模时忽略了输入电压和输出负载对变换器稳定工作点的影响,因此这种建模方法只在变换器扰动较小时才有效。当变换器工作点变化很大时该模型就不能准确反映系统的特性。用该模型设计的变换器的数字控制器也不能保证系统在大扰动下的稳定性。精确离散法是非线性模型,较别的模型可以更精确地描述变换器的离散工作特性,但这种非线性模型表达复杂,也不可以反映系统的高频分量,难以洞察参数变化对系统的影响,因此用于变换器闭环控制系统的设计有一定难度。准线性模型考虑了变换器工作点的变化,将系统的模型分为稳定点模型和该稳定点的扰动模型两个部分。这样就可以比较准确地反映变换器在大扰动时的工作特性。同时因为这种模型在每个稳定工作点附近是线性的,因此便于变换器控制系统的设计,且可以根据不同的稳定点设计不同的控制器参数,以实现自适应控制策略,使得控制具有很好的动态特性和稳定性。
3结论
本文以boost变换器为例,求解DC-DC变换器的平均离散模型、准线性离散模型和精确离散模型。分析比较了三种模型的各自的特点,探讨了其应用前景。分析结果表明准线性模型能精确的描述系统在各种扰动情况下的响应,且可以方便地应用于变换器的数字控制设计,实现变换器数字控制的自适应。
参考文献
[1]Petri Vallittu. Digital Control of Power Supply ——Opportunity and Constraints[A]. Proceedings of the 24th Annual Conference of the IEEE. 1998.562-567.
[2]Kocybik P F, Bateson K N. Digital Control of a ZVS Fullbridge DC-DC Converter[A]. IEEE APEC Rec. 1995.687-693.
[3]Tse C K. Quasilinear Modeling and Control of DC-DC Converters[J]. IEEE Trans on Power Electronics, 1992(7): 315-323.
[4]张占松(ZHANG Zhansong). 开关电源的原理与设计(Design of Switch Mode Power Supply)[M].北京:电子工业出版社(Beijing:Publishing House of Electronics Industry),1999.